题目内容
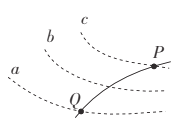
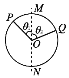
【题目】如图所示,在以R0为半径,O为圆心的圆形区域内存在磁场,直径MN左侧区域存在一匀强磁场,方向垂直于纸面向外,磁感应强度大小为B1;MN右侧区域也存在一匀强磁场,方向垂直于纸面向里,磁感应强度大小为B2,有一质量为m,电荷量为+q的带电粒子(不计重力)沿垂直于MN的方向从P点射入磁场,通过磁场区域后自Q点离开磁场,离开磁场时其运动方向仍垂直于MN。已知OP与MN的夹角为θ1,OQ与MN的夹角为θ2,粒子在左侧区域磁场中的运动时间为t1,粒子在右侧区域磁场中的运动时间为t2,则下列说法正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】AD
【解析】
AB.如图,设带电粒子的速度为v,它在MN左侧磁场的运动轨迹为圆弧PS,圆弧对应的圆心为C1,半径为R1,则有
![]()
且PC1平行于MN。
带电粒子进入MN右侧磁场的运动轨迹为圆弧SQ,圆弧对应的圆心为C2,半径为R2,则
![]()
且QC2平行于MN。
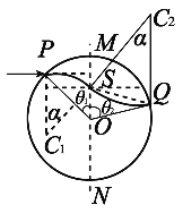
连接SC1、SC2,显然C1SC2为一直线,设![]() ,由图示的几何关系可得:
,由图示的几何关系可得:
![]() ,
,![]()
联立解得:
![]()
选项A正确, B错误;
CD.粒子在左侧区域磁场中的运动时间为
![]()
粒子在右侧区域磁场中的运动时间为
![]()
所以
![]()
选项D正确,C错误。
故选AD。

练习册系列答案
相关题目