题目内容
3. 如图,小球从水平地面A点以v1斜抛到竖直墙壁时速度v2恰好与墙壁垂直,已知A点距墙壁的距离为L,球与竖直墙的碰撞点与地面的高度为h,求v1和v2.
如图,小球从水平地面A点以v1斜抛到竖直墙壁时速度v2恰好与墙壁垂直,已知A点距墙壁的距离为L,球与竖直墙的碰撞点与地面的高度为h,求v1和v2.
分析 采用逆向思维,小球做平抛运动,根据高度求出平抛运动的时间,根据水平位移和时间求出初速度,解v2的大小,根据速度位移求出A点的竖直分速度,结合平行四边形定则求出A点的速度.
解答 解:采用逆向思维,小球做平抛运动,根据h=12gt2得,t=√2hg,
则v2=Lt=L√g2h.
A点的竖直分速度vy=√2gh,
根据平行四边形定则知,v1=√vy2+v22=√2gh+gL22h.
答:v1和v2的大小分别为√2gh+gL22h、L√g2h.
点评 本题采用逆向思维解决比较简捷,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
13. 如图所示,O为两个等量异种点电荷+q、-q连线的中点,P为连线中垂线上的任意一点,分别用UO、UP和EO、EP代表该电场中O、P两点的电势和场强的大小,则( )
如图所示,O为两个等量异种点电荷+q、-q连线的中点,P为连线中垂线上的任意一点,分别用UO、UP和EO、EP代表该电场中O、P两点的电势和场强的大小,则( )
 如图所示,O为两个等量异种点电荷+q、-q连线的中点,P为连线中垂线上的任意一点,分别用UO、UP和EO、EP代表该电场中O、P两点的电势和场强的大小,则( )
如图所示,O为两个等量异种点电荷+q、-q连线的中点,P为连线中垂线上的任意一点,分别用UO、UP和EO、EP代表该电场中O、P两点的电势和场强的大小,则( )| A. | UO>UP,EO>EP | B. | UO=UP,EO>EP | C. | UO<UP,EO>EP | D. | UO>UP,EO=EP |
11. 两个圆管道的半径均为R,通过直管道将它们无缝连接在一起.让一直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度略低于入口A.已知BC连线经过右侧圆管道的圆心,D点与圆管道的圆心等高,以下判断正确的有( )
两个圆管道的半径均为R,通过直管道将它们无缝连接在一起.让一直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度略低于入口A.已知BC连线经过右侧圆管道的圆心,D点与圆管道的圆心等高,以下判断正确的有( )
 两个圆管道的半径均为R,通过直管道将它们无缝连接在一起.让一直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度略低于入口A.已知BC连线经过右侧圆管道的圆心,D点与圆管道的圆心等高,以下判断正确的有( )
两个圆管道的半径均为R,通过直管道将它们无缝连接在一起.让一直径略小于管径的小球从入口A处无初速度放入,B、C、D是轨道上的三点,E为出口,其高度略低于入口A.已知BC连线经过右侧圆管道的圆心,D点与圆管道的圆心等高,以下判断正确的有( )| A. | 如果小球与管道间无摩擦,在D点处,管道的右侧会受到小球的压力 | |
| B. | 如果小球与管道间无摩擦,小球一定能从E点射出 | |
| C. | 如果小球与管道间有摩擦,且小球能运动到C点,此处管道对小球的作用力可能为零 | |
| D. | 如果小球与管道间有摩擦,小球不可能从E点射出 |
18.如果两个不在同一直线上分运动一个是匀速直线运动,另一个是匀变速直线运动,则合运动.
| A. | 一定是直线运动 | B. | 一定是曲线运动 | ||
| C. | 可能是匀速运动 | D. | 不可能是匀变速运动 |
8. (多选)为保证用户电压稳定在220V,变电所需适时进行调压,图甲为变压器示意图.保持输入电压U1不变,当滑动接头P上下移动时可改变输出电压.某次检测得到用户电压随时间t变化的曲线如图乙所示.以下正确的是( )
(多选)为保证用户电压稳定在220V,变电所需适时进行调压,图甲为变压器示意图.保持输入电压U1不变,当滑动接头P上下移动时可改变输出电压.某次检测得到用户电压随时间t变化的曲线如图乙所示.以下正确的是( )
 (多选)为保证用户电压稳定在220V,变电所需适时进行调压,图甲为变压器示意图.保持输入电压U1不变,当滑动接头P上下移动时可改变输出电压.某次检测得到用户电压随时间t变化的曲线如图乙所示.以下正确的是( )
(多选)为保证用户电压稳定在220V,变电所需适时进行调压,图甲为变压器示意图.保持输入电压U1不变,当滑动接头P上下移动时可改变输出电压.某次检测得到用户电压随时间t变化的曲线如图乙所示.以下正确的是( )| A. | u2=190√2 sin (50πt)V | |
| B. | u2=190√2 sin (100πt)V | |
| C. | 为使用户电压稳定在220 V,应将P适当下移 | |
| D. | 为使用户电压稳定在220 V,应将P适当上移 |
5. 如图为两个半径不同而内壁光滑的固定半圆轨道,质量相等的两个小球分别从与球心在同一水平高度的A、B两点由静止开始自由滑下,它们通过轨道最低点时,下列说法不正确的是( )
如图为两个半径不同而内壁光滑的固定半圆轨道,质量相等的两个小球分别从与球心在同一水平高度的A、B两点由静止开始自由滑下,它们通过轨道最低点时,下列说法不正确的是( )
 如图为两个半径不同而内壁光滑的固定半圆轨道,质量相等的两个小球分别从与球心在同一水平高度的A、B两点由静止开始自由滑下,它们通过轨道最低点时,下列说法不正确的是( )
如图为两个半径不同而内壁光滑的固定半圆轨道,质量相等的两个小球分别从与球心在同一水平高度的A、B两点由静止开始自由滑下,它们通过轨道最低点时,下列说法不正确的是( )| A. | 向心加速度相同 | B. | 对轨道的压力相等 | ||
| C. | 机械能相等 | D. | 速度相同 |
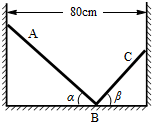 如图所示,在竖直平面内有两根质量相等的均匀细杆A和C,长度分别为60cm和40cm,它们的底端相抵于地面上的B点,另一端分别搁置于竖直墙面上,墙面间距为80cm,不计一切摩擦.系统平衡时两杆与地面的夹角分别为α和β,两侧墙面所受压力的大小分别为FA和FC,则FA等于FC(选填“大于”、“小于”或“等于”),夹角β=37°.
如图所示,在竖直平面内有两根质量相等的均匀细杆A和C,长度分别为60cm和40cm,它们的底端相抵于地面上的B点,另一端分别搁置于竖直墙面上,墙面间距为80cm,不计一切摩擦.系统平衡时两杆与地面的夹角分别为α和β,两侧墙面所受压力的大小分别为FA和FC,则FA等于FC(选填“大于”、“小于”或“等于”),夹角β=37°.
