题目内容

8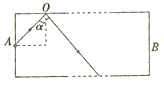．如图所示，AB为一直光导纤维，AB之间距离为s，使一光脉冲信号从光导纤维中间入射，射入后在光导纤维与空气的界面上恰好发生全反射，由A点传输到B点所用时间为t，求光导纤维所用材料的折射率n．

分析 光线在光导纤维与空气的界面上恰好发生全反射，入射角α等于临界角C，由几何关系可求得光在光纤中通过的总路程L，由v=$\frac{c}{n}$求出光在光纤中传播的速度，结合运动学知识列出方程，联立求解即可．

解答 解：据题图中入射角α等于临界角C．
根据全反射的规律和几何知识，可知光在光纤中通过的总路程为 L=$\frac{s}{sinα}$=$\frac{s}{sinC}$
又sinC=$\frac{1}{n}$，可得 L=ns
光在光纤中传播的速度为 v=$\frac{c}{n}$
则有 t=$\frac{L}{v}$=$\frac{ns}{\frac{c}{n}}$=$\frac{{n}^{2}s}{c}$
解得：
折射率 n=$\sqrt{\frac{ct}{s}}$
答：光导纤维所用材料的折射率n为$\sqrt{\frac{ct}{s}}$．

点评 本题考查了全反射知识的应用，关键要掌握全反射的条件，运用几何知识求总路程，也可以运用速度分解法求得光在光纤中水平分速度为 vsinα，由t=$\frac{s}{vsinα}$求解折射率n．

练习册系列答案
相关题目
18．某实验小组用图甲实验装置探究合力做功与动能变化的关系．铁架台竖直固定放置在水平桌面上，长木板一端放置在水平桌面边缘P处，另一位置放置在铁架台竖直铁杆上，使长木板倾斜放置．长木板P处放置一光电门，用光电计时器记录滑块通过光电门时挡光时间．
实验步骤是：
①用游标卡尺测出滑块的挡光宽度L，用天平测量滑块的质量m．
②平衡摩擦力：以木板放置在水平桌面上的P处为轴，调节长木板在铁架台上的放置位置，使滑块恰好沿木板向下做匀速运动．在铁架台竖直杆上记下此位置Q1，用刻度尺测出Q1到水平面的高度H．
③保持P位置不变，长木板一端放置在铁架台竖直杆Q2上．用刻度尺量出Q1Q2的距离h1，将滑块从Q2位置由静止释放，由光电门计时器读出滑块的挡光时间t1．
④保持P位置不变，重新调节长木板一端在铁架台上的放置位置，重复步骤③数次．
Ⅰ．滑块沿长木板由Q2运动到P的过程中，用测量的物理量回答下列问题（重力加速度已知为g）：
（1）滑块通过光电门的速度v=$\frac{L}{{t}_{1}}$；
（2）滑块动能的变化量△Ek=$\frac{1}{2}m\frac{{L}^{2}}{{{t}_{1}}^{2}}$；
（3）滑块克服摩擦力做的功Wf=mgH；
（4）合力对滑块做的功W合=mgh1．
Ⅱ．某学生以铁架台竖起杆上的放置位置到Q1的距离h为横坐标，以滑块通过光电门的挡光时间平方倒数$\frac{1}{{t}^{2}}$为纵坐标，根据测量数据在坐标中描点画出如图乙所示直线，直线延长线没有过坐标原点，其原因主要是平衡摩擦力倾角过大．
19．下列说法正确的是（　　）
A．发现中子的核反应方程是${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+${\;}_{0}^{1}$n
B．衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚形成的
C．比结合能越大，原子核中核子结合得越牢固，原子核越稳定
D．用某一频率的紫外线照射锌板表面能够发生光电效应，当增大这一频率紫外线的强度时，从锌板逸出的光电子的最大初动能也随之增大
E．氢原子由较高能级跃迁到较低能级时，将释放一定频率的光子
16．温室效应严重威胁着人类生态环境的安全．为了降低温室效应带来的负面影响，有的科学家受啤酒在较高压强下能够溶解大量二氧化碳的启发，设想用压缩机将二氧化碳送人海底，永久储存起来，海底压强很大，温度很低，海底深水肯定能溶解大量的二氧化碳，这样就为二氧化碳找到了一个永远的“家”，从而减弱温室效应．在将二氧化碳送入海底的过程中，以下说法不正确的是 （　　）
A．压缩机对二氧化碳做功，能够使其内能增大
B．二氧化碳与海水间的热传递能够使其内能减小
C．二氧化碳分子平均动能会减小
D．每一个二氧化碳分子平均动能都会减小
3．如图所示，水平路面CD的右侧有一长L1=2m的板M，一小物块放在板M的最右端，并随板一起向左侧固定的平台运动，板M的上表面与平台等高．平台的上表面AB长s=3m，光滑半圆轨道AFE竖直固定在平台上，圆轨道半径R=0.4m，最低点与平台AB相切于A点．当板M的左端距离平台L=2m时，板与物块向左运动的速度v0=8m/s．当板与平台的竖直墙壁碰撞后，板立即停止运动，物块在板上滑动，并滑上平台．已知板与路面的动摩擦因数u1=0.05，物块与板的上表面及轨道AB的动摩擦因数u2=0.1，物块质量m=1kg，取g=10m/s2．

（1）求物块进入圆轨道时对轨道上的A点的压力；
（2）判断物块能否到达圆轨道的最高点E．如果能，求物块离开E点后在平台上的落点到A点的距离；如果不能，则说明理由．
13．如图所示，质量为M、倾角为θ的斜面体A放于水平地面上，把质量为m的小滑块B放在斜面体A的顶端，顶端的高度为h．开始时两者保持相对静止，然后B由A的顶端沿着斜面滑至地面．若以地面为参考系，且忽略一切摩擦力，在此过程中，斜面的支持力对B所做的功为W．下面给出的W的四个表达式中，只有一个是合理的，你可能不会求解，但是你可以通过分析，对下列表达式做出合理的判断．根据你的判断，W的合理表达式应为（　　）
A．W=0B．W=-$\frac{{Mmh{{sin}^2}θ}}{{（{M+m}）（{M+m{{sin}^2}θ}）}}$g
C．W=$\frac{{Mmh{{cos}^2}θ}}{{（{M+m}）（{M+m{{sin}^2}θ}）}}$gD．W=-$\frac{M{m}^{2}h{cos}^{2}θ}{（M+m）（M+m{sin}^{2}θ）}g$
20．一物体静止在水平地面上，在竖直向上的拉力F的作用下开始向上运动，如图甲所示．在物体运动过程中，空气阻力不计，其机械能E与位移x的关系图象如图乙所示，其中曲线上点A处的切线的斜率最大．则（　　）
A．在x1处物体所受拉力最大
B．在x2处物体的速度最大
C．在x1〜x3过程中，物体的动能先增大后减小
D．在0〜x2过程中，物体的加速度先增大后减小
17．图1，某电厂要将电能输送到较远的用户，输送的总功率为9.8×104W，电厂的输出电压按如图2所示规律变化，为减少输送功率损失，先用一理想升压变压器将电压升高再输出，已知升压变压器原副线圈匝数比为$\frac{n_1}{n_2}=\frac{1}{28}$，输电导线的总电阻为50Ω．则下列说法正确的是（　　）
A．用户获得的交流电的频率为50Hz
B．升压变压器副线圈两端电压为9800$\sqrt{2}$V
C．通过输电导线R的电流为I=10A
D．由于输电线有电阻，输电过程中损失的功率为500W
18．用如图1所示的实验装置验证机械能守恒定律．

①实验中的电磁打点计时器，其电源应使用输出电压为6V的交流电（选填“交流电”或“直流电”）．
②先接通电源，使重锤从高处由静止开始下落，打点计时器每经过T时间在重锤拖着的纸带上打出一个点．其中A、B和C、D、E是两段连续打出的点，B、C间有一段纸带未画出．用刻度尺测量出各点间的距离分别为s1、s2、s3和s4，如图2所示．当地重力加速度为g．打点计时器在打出D点时重锤下落的速度vD=$\frac{{{s_3}+{s_4}}}{2T}$，若测得打出B点时重锤下落的速度为vB，则该实验需要验证的关系式是$g（{{s_2}+{s_3}}）=\frac{{{{（{{s_3}+{s_4}}）}^2}}}{{8{T^2}}}-\frac{v_B^2}{2}$．（用题目给出的物理量符号表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网