题目内容

（18分）如图所示，真空中以为圆心，半径r=0.1m的圆形区域内只存在垂直纸面向外的匀强磁场，圆形区域的最下端与xoy坐标系的x轴相切于坐标原点O，圆形区域的右端与平行y轴的虚线MN相切，在虚线MN右侧x轴的上方足够大的范围内有方向水平向左的匀强电场，电场强度E=1.0×105 N/C。现从坐标原点O沿xoy平面在y轴两侧各30°角的范围内发射速率均为v0=1.0×106m/s的带正电粒子，粒子在磁场中的偏转半径也为r=0.1m，已知粒子的比荷，不计粒子的重力、粒子对电磁场的影响及粒子间的相互作用力，求：

（1）磁场的磁感应强度B的大小；
（2）沿y轴正方向射入磁场的粒子，在磁场和电场中运动的总时间；
（3）若将匀强电场的方向改为竖直向下，其它条件不变，则粒子达到x轴的最远位置与最近位置的横坐标之差。

（1）（2）（3）

解析试题分析：（1）带电粒子在磁场中做匀速圆周运动，由                            ①
可得：                          ②
（2）分析可知，带电粒子运动过程如图所示，

由粒子在磁场中运动的周期              ③
可知粒子第一次在磁场中运动的时间：                  ④
              ⑤
粒子在电场中的加速度          ⑥
粒子在电场中减速到0的时间：                  ⑦
由对称性，可知运动的总时间：                ⑧
即                ⑨
（3）由题意分析可知，当粒子沿着y轴两侧300角射入时，将会沿着水平方向射出磁场区域，之后垂直虚线MN分别从P' 、Q'射入电场区，做类平抛运动，最终到达x轴的位置分别为最远位置P和最近位置Q。                                       ⑩

由几何关系P'到x轴的距离，               （11）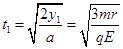

最远位置P坐标为           (12)
Q'到x轴的距离            (13)

最近位置Q坐标为                    (14)
所以，坐标之差为                      (15)
                  (16)
评分标准：①②每式2分，③④⑤⑥⑦⑧⑨⑩(11)(12)(13)(14)(15)(16)每式1分。
考点：本题考查带电粒子在电磁场中的运动

练习册系列答案
相关题目

如右图所示，在半径为R的圆形区域内充满磁感应强度为B的匀强磁场，MN是一竖直放置的感光板．从圆形磁场最高点P垂直磁场射入大量的带正电、电荷量为q、质量为m、速度为v的粒子，不考虑粒子间的相互作用力，关于这些粒子的运动以下说法正确的是(　　)

A．只要对着圆心入射，出射后均可垂直打在MN上
B．对着圆心入射的粒子，其出射方向的反向延长线不一定过圆心
C．对着圆心入射的粒子，速度越大在磁场中通过的弧长越长，时间也越长
D．只要速度满足，沿不同方向入射的粒子出射后均可垂直打在MN上

如图所示，圆心为原点、半径为的圆将平面分为两个区域，即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于平面的匀强磁场。平行于x轴的荧光屏垂直于平面，放置在直线的位置。一束质量为、电荷量为q、速度为的带正电粒子从坐标为（，0）的A点沿x轴正方向射入区域Ⅰ，粒子全部垂直打在荧光屏上坐标为（0，-2R）的点。若区域Ⅱ中加上平行于x轴的匀强电场，从A点沿x轴正方向以速度2射入区域Ⅰ的粒子垂直打在荧光屏上的N点。不考虑重力作用，求：

（1）在区域Ⅰ中磁感应强度B的大小和方向。
（2）在区域Ⅱ中电场的场强为多大？MN两点间距离是多少？

如图所示，垂直纸面的两平行金属板M、N之间加有电压，M板上O1处有一粒子源，可不断产生初速度为零的带正电粒子，粒子电荷量为q，质量为m，N板右侧是一半径为R的接地金属圆筒，圆筒垂直于纸面且可绕中心轴逆时针转动。O2为N板上正对O1的小孔，O3、O4为圆筒某一直径两端的小孔，开始时O1、O2、O3、O4在同一水平线上。在圆简上方垂直纸面放置一荧光屏，荧光屏与直线O1O2平行，圆筒转轴到荧光屏的距离OP=3R。不计粒子重力及粒子间相互作用。

（1）若圆筒静止且圆筒内不加磁场，粒子通过圆筒的时间为t，求金属板MN上所加电压U
（2）若圆筒内加垂直纸面向里的匀强磁场，磁感应强度大小为B，圆筒绕中心轴以某一角速度逆时针方向匀速转动，调节MN间的电压使粒子持续不断地以不同速度从小孔O2射出电场，经足够长的时间，有的粒子打到圆筒上被吸收，有的通过圆筒打到荧光屏上产生亮斑。如果在荧光屏PQ范围内的任意位置均会出现亮斑，。求粒子到达荧光屏时的速度大小的范围
（3）在第（2）问情境中，若要使进入圆筒的粒子均能从圆筒射出来，求圆筒转动的角速度

汤姆孙测定电子比荷的实验装置如图甲所示。从阴极K发出的电子束经加速后，以相同速度沿水平中轴线射入极板D1、D2区域，射出后打在光屏上形成光点。在极板D1、D2区域内，若不加电场和磁场，电子将打在P1点；若只加偏转电压U，电子将打在P2点；若同时加上偏转电压U和一个方向垂直于纸面向外、磁感应强度大小为B的匀强磁场（图中未画出），电子又将打在P1点。已知极板长度为L，极板间距为d。忽略电子的重力及电子间的相互作用。
 
（1）求电子射人极板D1、D2区域时的速度大小；
（2）打在P2点的电子，相当于从D1、D2中轴线的中点O’射出，如图乙中的O’ P2所示，已知试推导出电子比荷的表达式；
（3）若两极板间只加题中所述的匀强磁场，电子在极板间的轨迹为一段圆弧，射出后打在P3点。测得圆弧半径为2L、P3与P1间距也为2L，求图乙中P1与P2点的间距a。

如图所示，x轴的上方存在方向与x轴正方向成1350角的匀强电场，电场强度为E＝1×103V/m，x轴的下方存在垂直纸面向里的匀强磁场，磁感应强度B＝0.5T。有一个质量为m＝1×10-11kg，电荷量为q＝1×10-7C的带正电粒子，从坐标原点O以速度v＝2×103 m/s沿与x轴负方向成45°角方向进入磁场，设x轴上下方的电场和磁场区域足够大，不计粒子重力。求：

（1）粒子从O点出发到第一次经过x轴前，在磁场中运动轨迹的半径。
（2）粒子从O点出发到第一次经过x轴所经历的时间。
（3）粒子从O点出发到第四次经过x轴的坐标。

（18分）如图所示，圆心为原点、半径为R的圆将xOy平面分为两个区域，即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1。平行于x轴的荧光屏垂直于xOy平面，放置在坐标y＝-2．2R的位置。一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为（-R，0）的A点沿x正方向射入区域Ⅰ，当区域Ⅱ内无磁场时，粒子全部打在荧光屏上坐标为（0，-2．2R）的M点，且此时，若将荧光屏沿y轴负方向平移，粒子打在荧光屏上的位置不变。若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2，上述粒子仍从A点沿x轴正方向射入区域Ⅰ，则粒子全部打在荧光屏上坐标为（0.4R，-2．2R）的 N点。求：

（1）打在M点和N点的粒子运动速度v1、v2的大小。
（2）在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
（3）若将区域Ⅱ中的磁场撤去，换成平行于x轴的匀强电场，仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点，则电场的场强为多大？

（8分）在真空室内取坐标系xOy，在x轴上方存在两个方向都垂直于纸面向外的磁场区Ⅰ和II（如图），平行于x轴的虚线MM’和NN’是它们的边界线，两个区域在y方向上的宽度都为d、在x方向上都足够长．Ⅰ区和II区内分别充满磁感应强度为B和的匀强磁场．一带正电的粒子质量为m、电荷量为q，从坐标原点O以大小为v的速度沿y轴正方向射入Ⅰ区的磁场中．不计粒子的重力作用．

（1）如果粒子只是在Ⅰ区内运动而没有到达II区，那么粒子的速度v满足什么条件？粒子运动了多长时间到达x轴？
（2）如果粒子运动过程经过II区而且最后还是从x轴离开磁场，那么粒子的速度v又满足什么条件？并求这种情况下粒子到达x轴的坐标范围？

(15分)如图所示，在足够大的空间范围内，同时存在着竖直向上的匀强电场和垂直纸面向外的匀强磁场，电场强度为E，磁感应强度为B。足够长的斜面固定在水平面上，斜面倾角为。有一带电的小球P静止于斜面顶端A处，且恰好对斜面无压力。若将小球P以初速度水平向右抛出(P视为质点)，一段时间后，小球落在斜面上的C点。已知小球的运动轨迹在同一竖直平而内，重力加速度为g，求： 

(1)小球P落到斜面时速度方向与斜面的夹角及由A到C所需的时间t；
(2)小球P抛出到落回斜面的位移x的大小。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网