题目内容
17. 如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )
如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )| A. | 小物块与转台间的摩擦因数为μ=0.2 | |
| B. | 若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为1rad/s | |
| C. | 若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为$\sqrt{2}$rad/s | |
| D. | 若小物块质量变为原来2倍,则水平转台转动的角速度最大为2rad/s |
分析 当物块与平台恰好发生相对滑动时,靠最大静摩擦力提供向心力,结合牛顿第二定律分析判断.
解答 解:A、转台以角速度ω0=2rad/s转动时,物块恰好与平台发生相对滑动,根据牛顿第二定律得,$μmg=m{l}_{1}{{ω}_{0}}^{2}$,代入数据解得μ=0.2,故A正确.
B、若小物块与转轴间距离变为l2=1.0m,根据牛顿第二定律得,$μmg=m{l}_{2}{ω}^{2}$,解得最大角速度$ω=\sqrt{\frac{μg}{{l}_{2}}}=\sqrt{\frac{0.2×10}{1}}=\sqrt{2}rad/s$,故B错误,C正确.
D、由$μmg=m{l}_{2}{ω}^{2}$知,物块发生滑动时的临界角速度与质量无关,开始发生相对滑动的临界角速度为2rad/s,则质量变为原来的2倍,水平转台转动的角速度最大还是2rad/s,故D正确.
故选:ACD.
点评 解决本题的关键知道物块做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律分析求解,难度不大.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
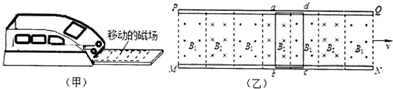
11.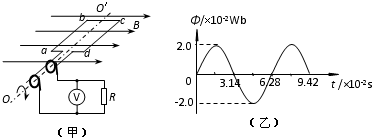 如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
 如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )| A. | 交流发电机产生的电动势的有效值为100$\sqrt{2}$V | |
| B. | 穿过线圈磁通量变化率的最大值为2×10-2V | |
| C. | 电路中交流电压表的示数为180V | |
| D. | 若规定t=0时的电流方向为正,则从此时开始发电机产生的电动势随时间变化的关系为e=200cos100t(V) |
5.物体在恒定的合力作用下做直线运动,在时间t1内动能由零增大到Ek1,在时间t2内动能由Ek1增加到2Ek1,设合力在时间t1内做的功为W1,冲量为I1,在时间t2内做的功是W2,冲量为I2,则( )
| A. | I1<I2 | B. | I1>I2 | C. | W1=W2 | D. | W1<W2 |
12.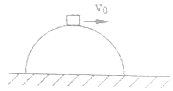 摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )
摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )
 摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )
摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )| A. | 摩托车立即离开球面做平抛运动,不再沿圆弧下滑 | |
| B. | v0=$\sqrt{gR}$ | |
| C. | 摩托车落地速度方向和水平地面成45°角 | |
| D. | 摩托车落地点离球顶水平位移$\sqrt{2}$R |
2.下列说法中正确的是( )
| A. | 原子核结合能越大,原子核越稳定 | |
| B. | 对黑体辐射的研究表明:随着温度的升高,辐射强度的最大值向波长较短的方向移动 | |
| C. | 核泄漏事故污染物Cs137能够产生对人体有害的辐射,其核反应方程式为$\left.\begin{array}{l}{137}\\{55}\end{array}\right.$Cs→$\left.\begin{array}{l}{137}\\{56}\end{array}\right.$Ba+x,可以判断x为正电子 | |
| D. | 一个氢原子处在n=4的能级,当它跃迁到较低能级时,最多可发出6种频率的光子 |
9.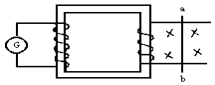 两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )
两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )
 两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )
两个线圈A、B绕在一个铁芯的两侧,分别跟电流表和导轨相连,导轨上垂直搁置一根金属棒ab,垂直导轨平面有一个匀强磁场,如图所示.在下列情况下能使电流计中有电流通过的是( )| A. | ab向右作匀速运动 | B. | ab向左作匀速运动 | ||
| C. | ab向竖直方向作加速运动 | D. | ab向左作加速运动 |
6.下列说法正确的是( )
| A. | 某气体的摩尔质量为M,分子质量为m,若1摩尔该气体的体积为V,则该气体单位体积内的分子数为$\frac{M}{mV}$ | |
| B. | 气体如果失去了容器的约束会散开,这是因为气体分子热运动的结果 | |
| C. | 只要技术手段足够先进,绝对零度可以达到的 | |
| D. | 利用浅层水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 | |
| E. | 物体温度升高,物体中分子热运动加剧,所有分子的动能都会增加 |
7.下列说法中正确的是( )
| A. | 天然放射现象的发现,揭示了原子核是由质子和中子组成的 | |
| B. | 氢原子的能级理论是玻尔在卢瑟福核式结构模型的基础上提出来的 | |
| C. | 汤姆孙通过对阴极射线的研究提出了原子核具有复杂的结构 | |
| D. | 卢瑟福的α粒子散射实验揭示了原子只能处于一系列不连续的能量状态中 |