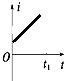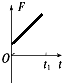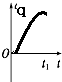题目内容
12.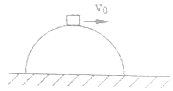 摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )
摩托车场地越野赛中常出现车飞离地面的惊险镜头,比赛时一辆摩托车冲上山坡可简化为如图所示的情景,山坡视为半径为R的半球,若摩托车在球顶时的速度为v0时,且此时摩托车对球顶恰无压力,则以下说法正确的是( )| A. | 摩托车立即离开球面做平抛运动,不再沿圆弧下滑 | |
| B. | v0=$\sqrt{gR}$ | |
| C. | 摩托车落地速度方向和水平地面成45°角 | |
| D. | 摩托车落地点离球顶水平位移$\sqrt{2}$R |
分析 摩托车对球顶恰无压力,仅受重力,做平抛运动,结合牛顿第二定律求出在最高点的速度大小.根据高度求出平抛运动的时间,结合初速度和时间求出平抛运动的水平位移,根据速度时间公式求出落地的竖直分速度,结合平行四边形定则求出落地的速度方向.
解答 解:A、摩托车对球顶恰无压力,仅受重力,做平抛运动,故A正确.
B、根据牛顿第二定律得,mg=$m\frac{{{v}_{0}}^{2}}{R}$,解得最高点的速度${v}_{0}=\sqrt{gR}$,故B正确.
C、根据R=$\frac{1}{2}g{t}^{2}$得,平抛运动的时间t=$\sqrt{\frac{2R}{g}}$,则落地的竖直分速度${v}_{y}=gt=\sqrt{2gR}$,根据平行四边形定则知,$tanα=\frac{{v}_{y}}{{v}_{0}}=\frac{\sqrt{2gR}}{\sqrt{gR}}=\sqrt{2}$,可知摩托车落地速度方向和水平地面的夹角不等于45度,故C错误.
D、水平位移x=${v}_{0}t=\sqrt{gR}•\sqrt{\frac{2R}{g}}=\sqrt{2}R$,故D正确.
故选:ABD.
点评 本题考查了圆周运动和平抛运动的基本运用,知道圆周运动最高点向心力的来源以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
6.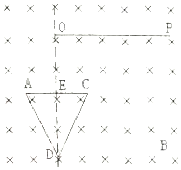 如图所示,边长为2a的等边三角形金属框和长为2$\sqrt{3}$a的金属棒OP处于同一平面内,O点在AC边等垂直平分线上,距离AC边的距离为$\sqrt{3}$a,磁感应强度为B的匀强磁场方向垂直金属框和导体棒所在平面向里,已知金属框的电阻为4R,金属棒的电阻为2R,现让金属棒绕O点以角速度ω沿顺时针匀速转动,已知金属框与金属棒接触良好,金属棒转至图中虚线位置时,下列说法正确的是( )
如图所示,边长为2a的等边三角形金属框和长为2$\sqrt{3}$a的金属棒OP处于同一平面内,O点在AC边等垂直平分线上,距离AC边的距离为$\sqrt{3}$a,磁感应强度为B的匀强磁场方向垂直金属框和导体棒所在平面向里,已知金属框的电阻为4R,金属棒的电阻为2R,现让金属棒绕O点以角速度ω沿顺时针匀速转动,已知金属框与金属棒接触良好,金属棒转至图中虚线位置时,下列说法正确的是( )
 如图所示,边长为2a的等边三角形金属框和长为2$\sqrt{3}$a的金属棒OP处于同一平面内,O点在AC边等垂直平分线上,距离AC边的距离为$\sqrt{3}$a,磁感应强度为B的匀强磁场方向垂直金属框和导体棒所在平面向里,已知金属框的电阻为4R,金属棒的电阻为2R,现让金属棒绕O点以角速度ω沿顺时针匀速转动,已知金属框与金属棒接触良好,金属棒转至图中虚线位置时,下列说法正确的是( )
如图所示,边长为2a的等边三角形金属框和长为2$\sqrt{3}$a的金属棒OP处于同一平面内,O点在AC边等垂直平分线上,距离AC边的距离为$\sqrt{3}$a,磁感应强度为B的匀强磁场方向垂直金属框和导体棒所在平面向里,已知金属框的电阻为4R,金属棒的电阻为2R,现让金属棒绕O点以角速度ω沿顺时针匀速转动,已知金属框与金属棒接触良好,金属棒转至图中虚线位置时,下列说法正确的是( )| A. | 金属棒产生的感应电动势为6Bωα2 | |
| B. | E、D两点的电势差大小为$\frac{9Bω{α}^{2}}{4}$ | |
| C. | 金属框所受安培力大小为$\frac{9Bω{α}^{2}}{2R}$ | |
| D. | 金属框上的电功率为$\frac{81{B}^{2}{ω}^{2}{α}^{4}}{8R}$ |
20.一矩形线圈在匀强磁场中匀速转动产生的电流瞬时值表达式为:i=10$\sqrt{2}$sin100πtA,则( )
| A. | 此交流的频率为50Hz | |
| B. | 此交流的峰值为10A | |
| C. | 用交流电流表测此电流,示数为10A | |
| D. | 用交流电流表测此电流,示数为14.1A |
7.电磁波无处不在,我们身边的广播、电视、移动通信都与电磁波有着密不可分的联系,Wi-Fi、非接触式公交卡、导航、雷达、微波加热、射电天文学、遥感遥测也都与电磁波有关.频率是电磁波的一个重要参量,不同频率的电磁波在空中互不干扰,保证了各项无线电应用的顺利开展.例如,我国自主建立的北斗导航系统所使用的电磁波频率约为1561MHz;家用微波炉加热食物所使用的电磁波频率约为2450MHz;家用5GWi-Fi所使用的电磁波频率约为5725MHz.对于家用5GWi-Fi的信号,下列说法中正确的是( )
| A. | 一定不会产生偏振现象 | |
| B. | 从一个房间穿越墙壁进入另一个房间后,频率保持不变 | |
| C. | 与北斗导航信号叠加时,将产生明显的干涉现象 | |
| D. | 与微波炉所使用的微波相比,更容易产生明显衍的射现象 |
17. 如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )
如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )
 如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )
如图所示,置于圆形水平转台上的小物块随转台转动.若转台以角速度ω0=2rad/s.转动时,物块恰好与平台发生相对滑动.现测得小物块与转轴间的距离l1=0.50m,设物块所受的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2. 则( )| A. | 小物块与转台间的摩擦因数为μ=0.2 | |
| B. | 若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为1rad/s | |
| C. | 若小物块与转轴间距离变为l2=1.0m,则水平转台转动的角速度最大为$\sqrt{2}$rad/s | |
| D. | 若小物块质量变为原来2倍,则水平转台转动的角速度最大为2rad/s |
4.以下关于固体和液体的说法中正确的是( )
| A. | 区分晶体与非晶体的最有效方法是看有没有一定的熔点 | |
| B. | 产生毛细现象时,液体在毛细管中一定上升 | |
| C. | 浸润液体呈凸液面,不浸润液体呈凹液面 | |
| D. | 液晶对不同颜色光的吸收强度随电场强度的变化而变化 |
1.一次小张去公园游玩,他向一处平静的水面丢进一颗石子,激起一圈圈水波,小张观察到,石子落点平静后,远处的水波依然在向更远扩散,下列说法正确的是( )
| A. | 石子落点处的水振动后,引起相邻的水依次振动形成了水波 | |
| B. | 石子落点处的水迁移到了远处,所以远处的水波可以继续传播 | |
| C. | 波源停止振动后,水波仍旧可以传播 | |
| D. | 波源停止振动后,远处的水由于获得了能量,所以还可以振动 |
2.下列说法中不符合史实的是 ( )
| A. | 天然放射性现象使人类认识到原子核是可分的 | |
| B. | 玻尔理论认为,原子中的核外电子轨道是量子化的 | |
| C. | 汤姆孙通过对阴极射线的研究,提出了原子具有复杂的结构 | |
| D. | 卢瑟福的α粒子散射实验揭示了原子核与核外电子具有等量的电荷量 |
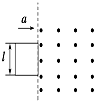 垂直纸面向外的匀强磁场左边界恰好与同一平面内的正方形金属导线框右边界重合,边界竖直,在外力作用下,导线框匀加速进入磁场区域,以顺时针方向为感应电流正方向,外力大小用F表示,感应电流的电功率用P表示,通过线框的电荷量用Q表示,感应电流大小用I表示,其中P-t图象为抛物线.则在线框匀加速进磁场的0-t1过程,这些量随时间变化的图象关系正确的是( )
垂直纸面向外的匀强磁场左边界恰好与同一平面内的正方形金属导线框右边界重合,边界竖直,在外力作用下,导线框匀加速进入磁场区域,以顺时针方向为感应电流正方向,外力大小用F表示,感应电流的电功率用P表示,通过线框的电荷量用Q表示,感应电流大小用I表示,其中P-t图象为抛物线.则在线框匀加速进磁场的0-t1过程,这些量随时间变化的图象关系正确的是( )