题目内容
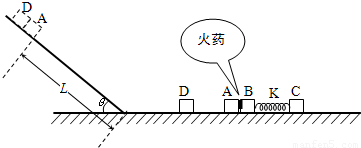
如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角 θ=37°,A、C、D滑块的质量为 mA=mC=mD=m=1kg,B滑块的质量 mB=4m=4kg(各滑块均视为质点).A、B间夹着质量可忽略的火药.K为处于原长的轻质弹簧,两端分别连接住B和C.现点燃火药(此时间极短且不会影响各物体的质量和各表面的光滑程度),此后,发现A与D相碰后粘在一起,接着沿斜面前进了L=0.8m 时速度减为零,此后设法让它们不再滑下.已知滑块A、D与斜面间的动摩擦因数均为 μ=0.5,取 g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)火药炸完瞬间A的速度vA;
(2)滑块B、C和弹簧K构成的系统在相互作用过程中,弹簧的最大弹性势能Ep.(弹簧始终未超出弹性限度).
【答案】分析:(1)欲求A的速度首先解决AD整体沿斜面上滑的初速度,应用动能定理即可求,然后利用动量守恒求出A的速度.
(2)B与C相互作用,当两者共速为V′时,弹簧弹性势能最大,由B、C系统动量守恒求出共同的速度,
由能量守恒知B与C动能的减少量就是弹簧的弹性势能.
解答:解:(1)设A和D碰完时的速度v1,AD系统沿斜面滑上,由动能定理,
-(mA+mD)gsinθ?L-μ(mA+mD)gcosθ?L=0- (mA+mD)
(mA+mD)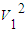
得:V1=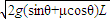
代入数据得V1=4m/s
炸药爆炸完毕时,设A的速度vA,由动量守恒定律有:
mAVA=(mA+mD)v1
得:vA=8 m/s
(2)炸药爆炸过程,对A和B系统,由动量守恒定律,设B获得的速度为vB,
有:-mAVA+mBVB=0
得:vB=2 m/s
B与C相互作用,当两者共速为V′时,弹簧弹性势能最大,由B、C系统动量守恒,
有:mBVB=(mB+mc)v′
解得:v′=1.6m/s
弹簧的最大弹性势能为:EP=
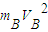 -
- (mB+mc)V′2
(mB+mc)V′2
代入数据得:EP=1.6 J
答:(1)火药炸完瞬间A的速度VA=8m/s;
(2)弹簧的最大弹性势能EP=1.6J
点评:本题是一道反复考查动量守恒、功能关系和动能定理的题目,关键是正确分析每个分过程列出方程,
特别是B与C的作用过程.是一道好题.
(2)B与C相互作用,当两者共速为V′时,弹簧弹性势能最大,由B、C系统动量守恒求出共同的速度,
由能量守恒知B与C动能的减少量就是弹簧的弹性势能.
解答:解:(1)设A和D碰完时的速度v1,AD系统沿斜面滑上,由动能定理,
-(mA+mD)gsinθ?L-μ(mA+mD)gcosθ?L=0-
 (mA+mD)
(mA+mD)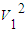
得:V1=
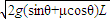
代入数据得V1=4m/s
炸药爆炸完毕时,设A的速度vA,由动量守恒定律有:
mAVA=(mA+mD)v1
得:vA=8 m/s
(2)炸药爆炸过程,对A和B系统,由动量守恒定律,设B获得的速度为vB,
有:-mAVA+mBVB=0
得:vB=2 m/s
B与C相互作用,当两者共速为V′时,弹簧弹性势能最大,由B、C系统动量守恒,
有:mBVB=(mB+mc)v′
解得:v′=1.6m/s
弹簧的最大弹性势能为:EP=

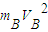 -
- (mB+mc)V′2
(mB+mc)V′2 代入数据得:EP=1.6 J
答:(1)火药炸完瞬间A的速度VA=8m/s;
(2)弹簧的最大弹性势能EP=1.6J
点评:本题是一道反复考查动量守恒、功能关系和动能定理的题目,关键是正确分析每个分过程列出方程,
特别是B与C的作用过程.是一道好题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 (2005?新洲区模拟)如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,A、B是两个质量均为m=1kg的小滑块(可看作质点),C为左端附有胶泥的质量不计的薄板,D为两端分别连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止下滑.(g=10m/s2,sin37°=0.6,cos37°=0.8)
(2005?新洲区模拟)如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,A、B是两个质量均为m=1kg的小滑块(可看作质点),C为左端附有胶泥的质量不计的薄板,D为两端分别连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N,方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止下滑.(g=10m/s2,sin37°=0.6,cos37°=0.8) (2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能.
(2013?辽宁一模)如图所示,粗糙斜面与水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角α=37°,水平面的M到N段是长度L1=0.3m的粗糙平面,N点的右边是光滑的.A、B是两个质量均为m=1kg的小滑块(可看作质点),置于N点处的C是左端附有胶泥的薄板(质量不计),D是两端分别与B和C连接的轻质弹簧,滑块A与斜面和与水平面MN段的动摩擦因数相同.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能向下匀速运动.现撤去F,让滑块A从斜面上距斜面底端L2=1m处由静止下滑(取g=10m/s2,sin37°=0.6,cos37°=0.8),求:滑块A与C接触并粘连在一起后,两滑块与弹簧所构成的系统在相互作用的过程中,弹簧的最大弹性势能. 如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.
如图所示,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾a=37°,A、B、C是三个小滑块(可看做质点),A、B的质量均为m=1kg,B的左端附有胶泥(质量不计),C的质量均为M=2kg,D为两端分别连接B和C的轻质弹簧.