Question

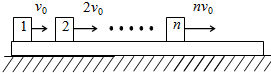
如图所示，平直轨道上有一车厢，质量为M，车厢以1.2m/s的速度向右匀速运动，某时刻与质量为m=

1

3

M的静止平板车相撞并连接在一起，车顶离平板车高为1.8m，车厢边缘有一钢球向前滑出，求钢球落在距离平板车左端何处？（平板车足够长，取g=10m/s²）

Answer 1

两车挂接时，因挂接时间很短，可以认为小钢球速度不变，以两车为组成的系统研究对象，设碰后共同速度为v，由动量守恒可得：
Mv₀=（M+m）?v
∴v=

Mv0

M+m

=

M

M+ 1 3 M

×1.2m/s=0.9m/s
设钢球落到平板车上所用时间为t．
由 h=

1

2

gt2得：t=

2h g

=

2×1.8 10

s=0.6s
t时间内平板车移动距离：s₁=vt．
钢球水平飞行距离：s₂=v₀t
则钢球距平板车左端距离：x=s₂-s₁=（v₀-v）t=（1.2-0.9）×0.6m=0.18m．
答：钢球落在平板车上距离左端距离0.18m处．