题目内容
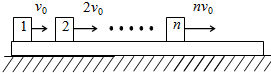
如图所示,一块足够长的木板,放在光滑水平面上,在木板上自左向右放有序号是1、2、3、…、n的木块,所有木块的质量均为m,与木板间的动摩擦因数均为μ,木板的质量与所有木块的总质量相等.在t=0时刻木板静止,第l、2、3、…、n号木块的初速度分别为vo、2vo、3vo、…、nvo,方向都向右.最终所有木块与木板以共同速度匀速运动.试求:
(1)所有木块与木板一起匀速运动的速度vn
(2)从t=0到所有木块与木板共同匀速运动经历的时间t
(3)第(n-1)号木块在整个运动过程中的最小速度vn-1.
(1)所有木块与木板一起匀速运动的速度vn
(2)从t=0到所有木块与木板共同匀速运动经历的时间t
(3)第(n-1)号木块在整个运动过程中的最小速度vn-1.

(1)木块与木板组成的系统动量守恒,以木块的初速度方向为正方向,
对系统,由动量守恒定律得:m(vo+2vo+3vo+…+nvo)=2nmvn,
解得:vn=
;
(2)第n号木块始终做匀减速运动,所以对第n号木块,
由动量定理得:-μmg t=mvn-mnvo,
解得:t=
;
(3)第(n-1)号木块与木板相对静止时,它在整个运动过程中的速度最小,设此时第n号木块的速度为v.
对系统,由动量守恒定律:m(vo+2vo+3vo+…+nvo)=(2n-1)m vn-1+mv ①
对第n-1号木块,由动量定理得:-μmg t′=m vn-1-m(n-1)vo②
对第n号木块,由动量定理得:-μmg t′=mv-mnvo③
由①②③式解得:vn-1=
.
答:(1)所有木块与木板一起匀速运动的速度vn为
;
(2)从t=0到所有木块与木板共同匀速运动经历的时间t=
;
(3)第(n-1)号木块在整个运动过程中的最小速度vn-1=
.
对系统,由动量守恒定律得:m(vo+2vo+3vo+…+nvo)=2nmvn,
解得:vn=
| (n+1)v0 |
| 4 |
(2)第n号木块始终做匀减速运动,所以对第n号木块,
由动量定理得:-μmg t=mvn-mnvo,
解得:t=
| (3n-1)v0 |
| 4μg |
(3)第(n-1)号木块与木板相对静止时,它在整个运动过程中的速度最小,设此时第n号木块的速度为v.
对系统,由动量守恒定律:m(vo+2vo+3vo+…+nvo)=(2n-1)m vn-1+mv ①
对第n-1号木块,由动量定理得:-μmg t′=m vn-1-m(n-1)vo②
对第n号木块,由动量定理得:-μmg t′=mv-mnvo③
由①②③式解得:vn-1=
| (n-1)(n+2)v0 |
| 4n |
答:(1)所有木块与木板一起匀速运动的速度vn为
| (n+1)v0 |
| 4 |
(2)从t=0到所有木块与木板共同匀速运动经历的时间t=
| (3n-1)v0 |
| 4μg |
(3)第(n-1)号木块在整个运动过程中的最小速度vn-1=
| (n-1)(n+2)v0 |
| 4n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目