题目内容
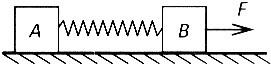
【题目】如图所示,空间存在竖直向上的匀强磁场,磁感应强度B=0.50T,两条光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.40m,左端接有阻值R=0.40Ω的电阻.一质量m=0.10kg、阻值r=0.10Ω的金属棒MN放置在导轨上.金属棒在水平向右的拉力F作用下,沿导轨做速度v=2.0m/s的匀速直线运动.求:
(1)通过电阻R的电流I;
(2)拉力F的大小;
(3)撤去拉力F后,电阻R上产生的焦耳热Q .
【答案】
(1)
MN棒产生的感应电动势 E=Blv=0.5×0.4×2 V=0.40V
通过电阻R的电流 ![]()
(2)
金属棒受到的安培力 FA=BIl=0.5×0.8×0.4N=0.16N
根据牛顿第二定律有 F﹣FA=0
所以拉力 F=0.16N
(3)
撤去拉力F后,金属棒做减速运动并最终静止,金属棒的动能全部转化为回路中的焦耳热.
在这段过程中,根据能量守恒定律有 ![]()
所以 ![]()
【解析】(1)MN棒产生的感应电动势 E=Blv=0.5×0.4×2 V=0.40V
通过电阻R的电流 ![]() (2)金属棒受到的安培力 FA=BIl=0.5×0.8×0.4N=0.16N
(2)金属棒受到的安培力 FA=BIl=0.5×0.8×0.4N=0.16N
根据牛顿第二定律有 F﹣FA=0
所以拉力 F=0.16N(3)撤去拉力F后,金属棒做减速运动并最终静止,金属棒的动能全部转化为回路中的焦耳热.
在这段过程中,根据能量守恒定律有 ![]()
所以 ![]()
【考点精析】关于本题考查的楞次定律,需要了解楞次定律适用于一般情况的感应电流方向的判定,而右手定则只适用于导线切割磁感线运动的情况,此种情况用右手定则判定比用楞次定律判定简便才能得出正确答案.

练习册系列答案
相关题目