题目内容
如图所示,长为L的轻绳一端连一质量为m的小球,另一端悬挂于O点,让A做圆锥摆运动,绳与竖直方向的夹角为θ.从A球经过图示位置开始计时,问经过多长时间从A初始位置的正上方与O等高的位置由静止释放的小球B自由下落中能与A相碰.

答案:略
解析:
解析:
|
A球在水平面内作匀速圆周运动,向心力  ,轨道半径R=Lsinθ,由牛顿第二定律有 ,轨道半径R=Lsinθ,由牛顿第二定律有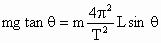 ,得 ,得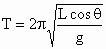 ;B下落时间 ;B下落时间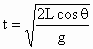 .因为T>t,所以当A通过初始位置后,经△t再释放B球,使A经一周期回到原位置时与B球相遇,有T=t+△t,即 .因为T>t,所以当A通过初始位置后,经△t再释放B球,使A经一周期回到原位置时与B球相遇,有T=t+△t,即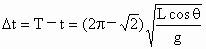 . .
该题是圆周运动与自由落体运动相结合的题目,小球 B在竖直方向上只受重力,做自由落体运动,小球A在水平面内匀速圆周运动的向心力由重力和绳的拉力的合力提供,两者相遇,A经历一个周期时间与B球在同一位置. |

练习册系列答案
相关题目
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点,且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点,且在P点受到轻杆向上的支持力 |
 (2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2
(2004?天津模拟)如图所示,长为l的轻杆一端固定一质量为m的小球,另一端有固定转轴O,杆可在竖直平面内绕转轴O无摩擦转动.已知小球通过最低点Q时,速度大小为v=2 如图所示,长为L的轻杆一端固定一个小球,另一端固定在光滑水平轴上,使小球在竖直平面内做圆周运动,设小球在过最高点A点的速度v,下列叙述中正确的是( )
如图所示,长为L的轻杆一端固定一个小球,另一端固定在光滑水平轴上,使小球在竖直平面内做圆周运动,设小球在过最高点A点的速度v,下列叙述中正确的是( ) 如图所示,长为L的轻绳一端固定于O点,另一端系一个小球.现使小球在竖直平面内做圆周运动,P是圆周轨道最高点,Q是轨道最低点.已知重力加速度为g.若小球刚好能够通过最高点P,则以下判断正确的是( )
如图所示,长为L的轻绳一端固定于O点,另一端系一个小球.现使小球在竖直平面内做圆周运动,P是圆周轨道最高点,Q是轨道最低点.已知重力加速度为g.若小球刚好能够通过最高点P,则以下判断正确的是( ) 如图所示,长为L的轻杆两端各连一个质量均为m的小球(半径可以忽略不计),以它们的中点为轴,在竖直平面内做匀速圆周运动,转动周期为T=2π
如图所示,长为L的轻杆两端各连一个质量均为m的小球(半径可以忽略不计),以它们的中点为轴,在竖直平面内做匀速圆周运动,转动周期为T=2π