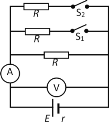
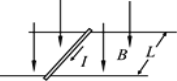
��Ŀ����
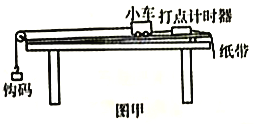
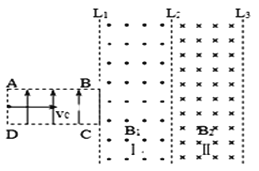
����Ŀ����ͼ��ʾ�������㹻���⻬ƽ�н���������l=0.9m����ˮƽ��н���=30��������������abcd������ǿ�ų����Ÿ�Ӧǿ��B=2T������ֱ��б�����ϣ��ס���������������ͬ�������ΪR=4.86���Ľ����ˣ���ֱ�ڵ�����á������ڴų����ϱ߽�ab���������ڼ��Ϸ�l�����ֽ����������ɾ�ֹͬʱ�ͷţ��������ڼ���ʩ��һ���ص��췽�������F����ʼ����a=5m/s2�ļ��ٶ��ص����ȼ����˶����ҽ���ų�ʱǡ���������˶���g=10m/s2�����㣺

(1)ÿ�������˵�����m��
(2)����F�����ֵ��
(3)�ҵ���ų��±߽�ʱ���˼�ľ��뼰�Ҵ����ų��Ĺ����е�·������������
���𰸡���1��0.2kg��2��1N��3��0.225m��0.9J
��������
��1���������ҽ���ų�ǰ�����ٶ�Ϊ����ȼ���ֱ���˶�������ţ�ٵڶ����������ٶȣ������˶���ʽ������ų����ٶȣ��ҽ���ų���������ֱ���˶�����ƽ�����������ÿ������������������2��������»��ļ��ٶ���ȣ���֪�����ڴų��л���ʱ���һ�δ����ų�������ţ�ٵڶ������г�F�ı���ʽ�������ȼ���ֱ���˶���v����������F�������cdλ��ʱ��������ٶ����F���3���׳���ų������ȼ����˶������ڴų����������˶������˶���ʽ����ҵ���ų��±߽�ʱ���˼�ľ��룻�Ҵ����ų����̲��������������һ�е�ܵļ�С����
��1��������ã��ҽ���ų�ǰ�����ٶ�Ϊ����ȼ���ֱ���˶������ٶȣ�
![]() =10��sin30��=5m/s2��
=10��sin30��=5m/s2��
�ҽ���ų�ʱ���ٶȣ�![]() =3m/s
=3m/s
�ҽ���ų���������ֱ���˶�����ƽ�������ã�![]()
��ã�m=0.2kg
��2��������»��ļ��ٶ���ȣ���֪�����ڴų��л���ʱ���һ�δ����ų�������ڴų����ܵ��İ�������![]()
��ţ�ٵڶ����ɿɵã�![]()
�����ȼ���ֱ���˶���![]() ����������
����������![]() �������cdλ��ʱ��������ٶ����F���ʱ���ٶ�
�������cdλ��ʱ��������ٶ����F���ʱ���ٶ�![]() ��
��
��������ݽ�ã�F=1N
��3���Ҵӽ���ų�������ų��±߽��ʱ��![]() ��
��
���ҽ���ų�ʱ���պó���ų����ٶ�Ϊv=3m/s���׳���ų���ļ��ٶ���Ϊ5m/s2����t=0.3s�ڵ�λ��![]() ��
��
���ʱ�����������![]()
�Ҵ����ų����̲��������������һ�е�ܵļ�С����
![]()