题目内容
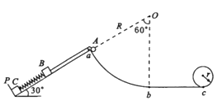
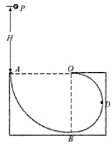
【题目】如图所示,ABDO是处于竖直平面内的光滑轨道,AB是半径为R=15m的1/4圆周轨道,半径OA处于水平位置,BDO是半径为r=7.5m的半圆轨道,D为BDO轨道的中央。一个小球从A点正上方距A点H=10m处的P点自由落下,经A点进入竖直平面内的轨道,取g=10m/s2,不计空气阻力。
(1)求小球经过D点时对轨道的压力的大小是重力的多少倍?
(2)试讨论此球能否到达BDO轨道的O点,并说明理由。
(3)小球沿轨道运动后再次落到轨道上的速度的大小是多少?
【答案】(1)![]() (2)能(3)
(2)能(3)![]()
【解析】
(1)从P到D由动能定理得:
![]()
由圆周运动知识得:
![]()
解得:![]() ;
;
(2) 设小球能够沿竖直半圆轨道运动到O点的最小速度为vc,有:
![]()
小球至少应从Hc高处落下,![]()
解得:![]()
由H>HC,小球可以通过O点;
(3) 小球从O点水平飞出后打在圆弧轨道上时间为t
这个过程小球的水平位移为x=v0t
竖直位移为![]()
由几何知识得:![]()
解得t=1s
物体竖直方向速度vy=gt=10m/s
落在圆弧上速度![]() 。
。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目