Question

【题目】如图，粗糙直轨道AB与水平方向的夹角θ＝37°；曲线轨道BC光滑且足够长，它们在B处光滑连接。一质量m＝0.2kg的小环静止在A点，在平行于AB向上的恒定拉力F的作用下，经过t＝0.8s运动到B点，立即撤去拉力F，小环沿BC轨道上升的最大高度h=0.8m。已知小环与AB间动摩擦因数μ＝0.75。（g取10m/s2，sin37°＝0.6，cos37°＝0.8）求：

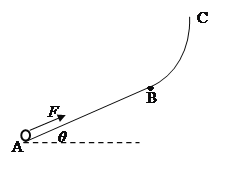
（1）小环上升到B点时的速度大小；

（2）拉力F的大小；

（3）简要分析说明小环从最高点返回A点过程的运动情况。

Answer 1

【答案】(1) 4m/s (2) 3.4N (3) 小环从最高点返回B点过程中，只有重力做功，机械能守恒 ，小环做加速运动，回到B点时速度大小为4m/s。小环由B向A运动过程中，根据小环受力有F合=mgsinθ—μmgcosθ =0，小环在BA段以4m/s平行BA向下匀速直线运动

【解析】试题分析：因BC轨道光滑，小环在BC上运动时只有重力做功，其机械能守恒，根据机械能守恒定律求解小环在B点时的速度大小；小环在AB段运动过程，由牛顿第二定律和运动学公式结合求解拉力F的大小。

（1）因BC轨道光滑，小环在BC上运动时只有重力做功，机械能守恒，即小环在B处与最高处的机械能相等，且在最高处时速度为零，以B点为零势能点，

根据机械能守恒定律：

代入数据得小环在B点速度：vB＝4m/s

（2）小环在AB段受到恒力作用，做初速度为零的匀加速直线运动

所以有vB＝at

代入数据得a=5m/s2

小环受力如图：

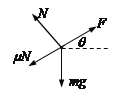
根据小环受力，由牛顿第二定律：F合=ma 即F—mgsinθ—f=ma

其中： f=μN=μmgcosθ

可得：F=mgsinθ+μmgcosθ+ma

代入数据得 F=3.4N

（3）小环从最高点返回B点过程中，只有重力做功，机械能守恒 ，小环做加速运动，

回到B点时速度大小为4m/s。小环由B向A运动过程中，根据小环受力有：F合=mgsinθ—μmgcosθ =0，小环在BA段以4m/s平行BA向下匀速直线运动。