题目内容
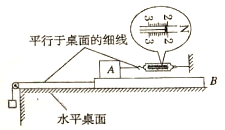
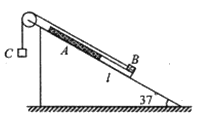
【题目】如图所示,在倾角为37°的足够长的光滑斜面上,放一质量为 mA=0.2kg的薄板A, A板上、下段由不同材料构成,下段表面光滑,长度 l=3m,上段表面粗糙;质量为 mB=2.0kg 的金属块 B(视为质点)位于A的最下端,B与 A上段间的动摩擦因数μ=0.1;质量为 mC=1.2kg 的物块 C通过轻线绕过定滑轮与 B相连。忽略滑轮质量及轴间的摩擦,A、B间最大静摩擦力可认为等于滑动摩擦力。开始时,整个系统在外力作用下,处于静止状态,轻线被拉直。(sin370=0.6, cos370=0.8,g=10m/ s2。)求:
(1)撤去外力的瞬间,A、 B、 C的加速度分别是多大;
(2)B刚到达A的粗糙部分时,A、 B、 C的加速度分别是多大;
(3)撤去外力后的整个过程中,因摩擦产生的热量Q,绳足够长,B始终没滑出A板
【答案】(1)![]() (2)
(2)![]() (3)11.52J
(3)11.52J
【解析】
(1)由于mBgsin37°=mcg=12N 所以,撤去外力的瞬间aB=ac=0
对薄板A,有mAgsin37°=mAaA
得aA=6m/s2
(2)由于斜面和A板下段表面都光滑,撤去外力后,A板从静止开始向下做匀加速运动,只要金属块B在A板下段表面上,B、C就保持静止不动.A板运动到金属块B在其上段表面上后,B和C受滑动摩擦力作用将一起以相同大小的加速度做加速运动.设A板上段刚滑到B下方时速度为vA,则vA2=2aAl
解得vA=6m/s
B在A板上端表面时,设A板加速度为aA1,B和C加速度为aB1,轻线拉力为F,则
mAgsin37°-μmBgcos37°=mAaA
mBgsin37°+μmBgcos37°-F=mBaB1
F-mCg=mCaB1
解得aA1=-2m/s2,aB1 =aC1=0.5m/s2
(3)A、B、C最终达到速度相等.假设速度相等之后,A、B间的静摩擦力f小于最大静摩擦力fm,即A、B相对静止,A、B、C三者加速度大小相同,设为a0,则
(mA+mB)gsin37°-mCg=(mA+mB+mC)a0
mAgsin37°-f=mAa0
a0=0.5m/s2,f=1.1N
fm=μmBgcos37°=1.6N
即f<fm,假设成立,之后A、B相对静止.
设A、B、C达到相等速度v1所需时间为t,则
v1=vA+aA1t=aB1t
解得t=2.4s,v1=1.2m/s
设在时间t内,A通过的距离是xA,B和C通过的距离是xB,则
xA=![]() (vA+v1)t
(vA+v1)t
xB=![]() v1t
v1t
解得xA=8.64m,xB=1.44m
Q=μmBg(xA-xB)cos37°
Q=11.52J

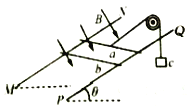
【题目】某同学做“探究弹力和弹簧伸长量的关系”的实验,设计了如下图所示的 实验装置,将待测弹簧的一端固定在铁架台上,然后将毫米刻度尺放置在弹黄—侧,并使弹簧另一端的指针恰好落在刻度尺上。他先测出不挂钩码时弹簧的自然长度,然后在弹簧下端依次挂1、2、3、4、5个钩码,测出弹簧相应的总长度。每只钩码的质量都是10g。实验数据见下表。(g取10N/kg)
钩码质量m/g | 0 | 10 | 20 | 30 | 40 | 50 |
弹簧总长度l/cm | 3.00 | 3.50 | 4.00 | 4.50 | 5.00 | 5.50 |
弹力大小F/N | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
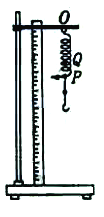
(1)关于本实验,下列说法正确的是_________。
A.悬吊钩码时,应在钩码静止后再读数
B.应在弹簧的弹性限度范围内进行测量
C.在安装刻度尺时,必须使刻皮尺保持竖直状态
D.在测量弹簧原长时,应将弹簧平放在水平桌面上,使其自然伸长,并测出其长度
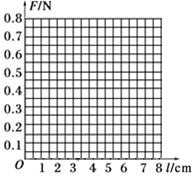
(2)根据上逆实验数据,在图9所不的坐标纸上,作出弹簧弹力大小F跟弹簧总长度l之间的关系图象,并求出该弹簧的劲度系数k=_________N/m。
(3)如果实验时将指针固定在图8中P点上方的Q处,测出弹簧的劲度系数与弹簧的劲度系数的真实值相比,可能_________(选填“偏大”或“偏小”或“不变”)。
(4)一个实验小组在“探究弹力和弹簧伸长的关系”的实验中, 使用两条不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图10所示。下列表述正确的是_________。
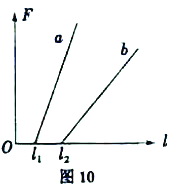
A.a的原长比b的短
B.a的劲度系数比b的小
C.a的劲度系数比b的大
D.测得的弹力与弹簧的长度成正比