题目内容
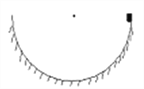
【题目】如图所示，质量m=10kg的物体从光滑曲面上高度H=0.8m处由静止释放，到达曲面底端时以水平方向的速度进入水平传送带．传送带由一电动机驱动，传送带的上表面匀速向左运动，运动速率为v=1m/s．已知物体与传送带间的动摩擦因数μ=0.1．（物体m可视为质点，g取10m/s2）求：
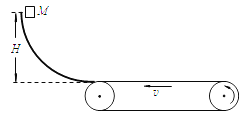
（1）物体滑上传送带时的速度；
（2）若两皮带轮之间的距离是L=6m，物体滑上传送带后立刻移走光滑曲面，物体将从哪一边离开传送带？通过计算说明你的结论．并求物体m从滑上到离开传送带摩擦产生的热量．
【答案】（1）4m/s（2）80J
【解析】试题分析：（1）根据动能定理求得物体滑上传送带上时的速度；
（2）由牛顿第二定律可求得物体在传送带上运动时的加速度，则可求得物体的运动情况，进而确定小球从哪一端离开；摩擦力与物体和传送带之间的相对滑动位移的乘积转化为热量．
（1）物体沿圆弧曲面下滑时只有重力做功，根据动能定理有
解得物体到达传送带时的速度为： 
（2）若物体从右端离开传送带，由动能定理有： 
代入数据解得： 
，故物体离开传送带
物体在传送带上相对于地面做匀减速直线运动，滑出传送带时间为t， 
可得加速度为： 
物体运动时间为： 
内传送带运动的位移为： 
所以物体与传送带间相对滑动的位移为： 
可得摩擦产生的热量为： 
练习册系列答案
相关题目
