Question

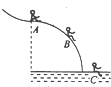
【题目】如图所示，M为固定在水平桌面上的有缺口的方形木块，abcd为半径是R的四分之三光滑圆弧形轨道，a为轨道最高点，de面水平且有一定长度.今将质量为m的小球在d点的正上方高为h处由静止释放，其自由下落到d处切入轨道内运动，不计空气阻力.则以下正确的是

A. 调节h，可以使小球经过轨道后返回释放点

B. 无论怎样改变h，都不可能使小球通过a点后落回轨道内

C. 调节h，可以使小球通过a点做自由落体运动

D. 只要改变h，就能使小球通过a点后，既可以落回轨道内又可以落到de面上

Answer 1

【答案】AB

【解析】若调节h使得小球进入轨道后能在bd以下运动，则可使小球经过轨道后返回释放点，选项A正确；小球恰能通过a点的条件是小球的重力提供向心力，根据牛顿第二定律：mg=m，解得：v=；根据动能定理：mg（h-R）=mv2，得：h=1.5R，可知只有满足h≥1.5R，释放后小球才能通过a点；小球离开a点时做平抛运动，用平抛运动的规律，水平方向的匀速直线运动：x=vt；竖直方向的自由落体运动：R=gt2，解得：x=R＞R，故无论怎样改变h的大小，都不可能使小球通过a点后落回轨道内，小球通过a点不可能做自由落体运动。只要改变h的大小，就能改变小球到达a点的速度，就有可能使小球通过a点后，落在de之间或之外。故B正确，CD错误。故选AB。