��Ŀ����
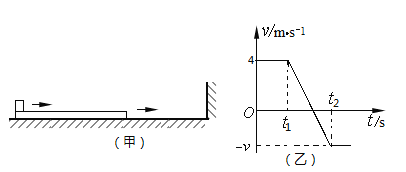
����Ŀ����ͼ��ʾ�����ʵ���һ�˹̶�����һ����һ����Ϊ![]() �����ڴֲ���ֱ�̶���
�����ڴֲ���ֱ�̶���![]() ����Բ������������ˮƽ�Ҵ���ԭ����Բ����
����Բ������������ˮƽ�Ҵ���ԭ����Բ����![]() ���ɾ�ֹ��ʼ�»�������
���ɾ�ֹ��ʼ�»�������![]() �����ٶ������
�����ٶ������![]() �����ٶ�Ϊ�㣬
�����ٶ�Ϊ�㣬 ![]() ����Ϊ����������Բ����
����Ϊ����������Բ����![]() �����һ��ֱ���ϵ��ٶ�
�����һ��ֱ���ϵ��ٶ�![]() ����ǡ���ܻص�
����ǡ���ܻص�![]() ������Ϊ����������֪����ʼ���ڵ��Է�Χ�ڣ��������ٶ�Ϊ
������Ϊ����������֪����ʼ���ڵ��Է�Χ�ڣ��������ٶ�Ϊ![]() ����Բ���� ��
����Բ���� ��

A. �������У����ٶ�һֱ��С
B. �������У��˷�Ħ�������Ĺ�Ϊ![]()
C. ��C�������ɵĵ�������Ϊ![]()
D. ���������������п˷�Ħ����������ͬ
���𰸡�D
��������Բ����A���ɾ�ֹ��ʼ�»�������B�����ٶ������B���ļ��ٶ�Ϊ�㣬����C�����ٶ�Ϊ�㣬����Բ�����������˶������������˶������Լ��ٶ��ȼ�С��������A�����ڹ��̢��̢��У�Բ������ͬһλ�����ܵ�Ħ������С��ȣ���֪�����������У��˷�Ħ����������ͬ����ΪWf���о����̢����ö��ܶ�����ʽ�ã� mgh-Wf-W��=0
�о����̢����ö��ܶ�����ʽ�ã�-mgh��-Wf+W��=0-![]() mv2��������ã��˷�Ħ�������Ĺ�Ϊ��Wf=
mv2��������ã��˷�Ħ�������Ĺ�Ϊ��Wf=![]() mv2��W��=mgh-
mv2��W��=mgh-![]() mv2��������C�������ɵĵ�������Ϊ Ep=W��=mgh-
mv2��������C�������ɵĵ�������Ϊ Ep=W��=mgh-![]() mv2����BC����D��ȷ����ѡD.
mv2����BC����D��ȷ����ѡD.