题目内容
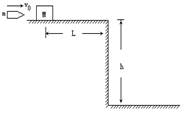
如图所示,高为h=10m的平台上,放一质量为M=9.9kg的木块,它与平台边缘的距离为L=1m.今有一质量m=0.1kg的子弹,以水平向右的速度
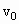 射入木块(时间极短),并留在木块中,木块向右滑行并冲出平台,最后落在离平台边缘水平距离x=
射入木块(时间极短),并留在木块中,木块向右滑行并冲出平台,最后落在离平台边缘水平距离x=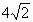 m处,已知木块与平台间的动摩擦因数为μ=
m处,已知木块与平台间的动摩擦因数为μ=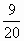 ,g=10m/
,g=10m/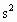 .求:
.求:(1)木块离开平台边缘时的速度;
(2)子弹射入木块的初速度
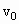 .
.(1)4m/s; (2)500m/s.
(1)设木块从离开平台到落地的时间为t,则有
h=
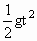 ,得t=
,得t=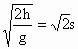 .
.又设木块离开平台时的速度为v,由已知可得:
x=vt,即v=
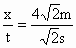 =4m/s,
=4m/s,所以木块离开平台边缘时的速度为4m/s;
(2)设子弹射入木块后的共同速度为
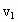 ,
,根据动能定理有:
-μ(M+m)gL=
 (m+M)
(m+M)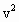 -
- (M+m)
(M+m)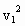
得:
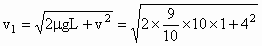 m/s=5m/s,
m/s=5m/s,子弹射入木块,由于相互作用时间很短,对子弹和木块组成的系统动量守恒,则由动量守恒定律可得:
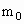 =(M+m)
=(M+m)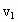 ,
,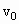 =500m/s,
=500m/s,即子弹射入木块的初速度为500m/s.

练习册系列答案
相关题目
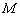 的木块在光滑水平面上以速度
的木块在光滑水平面上以速度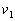 向右运动,质量为
向右运动,质量为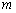 的子弹以速度
的子弹以速度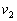 水平向左射入木块,要使木块停下来,必须发射的子弹数目为(子弹留在木块中不穿出):( )
水平向左射入木块,要使木块停下来,必须发射的子弹数目为(子弹留在木块中不穿出):( )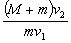
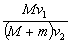

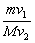
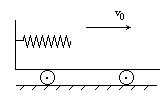
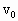 向右匀速运动,物块A与其左侧的车面的动摩擦因数为
向右匀速运动,物块A与其左侧的车面的动摩擦因数为 ,与其余部分车面间无摩擦.在车匀速运动时,距沙面H高处有一质量为m的泥球自由下落,恰好落在沙箱中,试求:
,与其余部分车面间无摩擦.在车匀速运动时,距沙面H高处有一质量为m的泥球自由下落,恰好落在沙箱中,试求: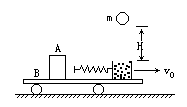
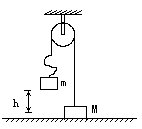
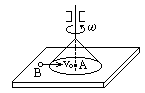
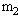 的小球A,现有一质量为
的小球A,现有一质量为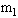 的小球B以速度
的小球B以速度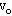 正对A运动,在圆环缺口转至某位置时,B球刚好通过缺口运动至中心与A发生正碰,碰后二球粘在一起又恰好从缺口处离开圆环,则圆环的角速度为多大?
正对A运动,在圆环缺口转至某位置时,B球刚好通过缺口运动至中心与A发生正碰,碰后二球粘在一起又恰好从缺口处离开圆环,则圆环的角速度为多大?