题目内容
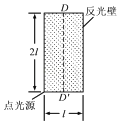
【题目】如图所示，一弹射游戏装置由安装在水平台面上的固定弹射器、竖直圆轨道（在最低点E分别与水平轨道
和
相连）、高度h可调的斜轨道
组成。游戏时滑块从O点弹出，经过圆轨道并滑上斜轨道。全程不脱离轨道且恰好停在B端则视为游戏成功。已知圆轨道半径
，
长
，
长
，圆轨道和
光滑，滑块与、之间的动摩擦因数
。滑块质量m=2g且可视为质点，弹射时从静止释放且弹簧的弹性势能完全转化为滑块动能。忽略空气阻力，各部分平滑连接。求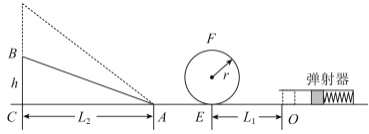
（1）滑块恰好能过圆轨道最高点F时的速度
大小；
（2）当
且游戏成功时，滑块经过E点对圆轨道的压力
大小及弹簧的弹性势能
；
（3）要使游戏成功，弹簧的弹性势能
与高度h之间满足的关系。
【答案】(1) 
(2) 
(3) 
【解析】
（1）滑块恰过F点的条件：
解得：
（2）滑块从E到B，动能定理：
在E点根据牛顿第二定律：
解得：
从O到B点，根据能量守恒定律：
解得：
（3）滑块恰能过F点的弹性势能：
到B点减速到0：
解得：
能停在B点，则：
解得：
，此时
从O到B点：
其中
练习册系列答案
相关题目
