题目内容
【题目】如图所示,水平传送带水平段长l=3m,两皮带轮半径均为r=5cm,距地面高度h=3.2m,此时传送带静止。与传送带等高的光滑平台上,有一个可看成质点的小物体以v0的初速度滑上传送带,从传送带的右端飞出做平抛运动,水平射程是1.6m。已知物块与传送带间的动摩擦因数为0.2, 取重力加速度g为10m/s2, 求:
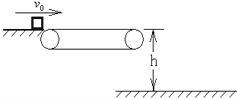
(1)物体的初速度v0?
(2)保持其它条件不变,为使物块作平抛运动的水平射程最大,则皮带轮至少应以多大的角速度转动?
(3)如要使物体的水平射程为2.4m,皮带轮的角速度是多少?
【答案】(1)4m/s(2)![]() (3)
(3)![]()
【解析】
根据平抛运动的规律求出平抛运动的初速度,结合牛顿第二定律和速度位移公式求出物体的初速度;
当物块一直做匀加速运动的时,水平射程最大,根据牛顿第二定律和速度位移公式求出平抛运动的最大速度,从而根据线速度与角速度的关系求出最小的角速度的大小。
(1)物体从传送带的右端飞出做平抛运动,则平抛运动的时间为
![]()
初速度为:![]()
物体滑上传送带后做匀减速运动,对此运用动能定理得:
![]()
解得:![]() ;
;
(2) 平抛运动的时间一定,当物体在传送带一直加速时,获得的速度最大,平抛运动的水平射程最大,物体获得的最大速度为v3
由动能定理:![]()
代入解得:![]()
则转动的角速度为![]() ;
;
(3) 要使物体的水平射程为2.4m,则平抛运动的初速度为
![]()
所以物体滑上传送带也做匀减速运动,当速度减至v2时,与传送带做匀速运动
则传送带的速度也为v2,则皮带轮的角速度是![]() 。
。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目