题目内容
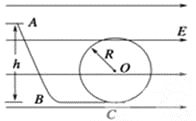
【题目】如图所示的装置是在竖直平面内放置光滑的绝缘轨道，处于水平向右的匀强电场中，一带负电荷的小球从高h的A处静止开始下滑，沿轨道ABC运动后进入圆环内作圆周运动．已知小球所受到电场力是其重力的3/4，圆环半径为R，斜面倾角为θ＝53°，SBC＝2R.若使小球在圆环内能作完整的圆周运动，h至少为多少？
【答案】10R
【解析】试题分析：小球所受的重力和电场力都为恒力，故两力可等效为一个力F，如图所示，可知F=
mg，方向与竖直方向夹角为37°，偏左下；从图中可知，做完整的圆周运动的临界条件是恰能通过D点，若球恰好能通过D点，则达到D点时小球与圆环间的弹力恰好为零，由圆周运动知识得：
即：
选择A点作为初态，D点为末态，由动能定理有： mg（h-R-Rcos37°）-
mg（htan37°+2R+Rsin37°）=
代入数据：mg（h-1.8R）-mg（h+2.6R）=
解得：h=10R
练习册系列答案
开心蛙口算题卡系列答案
相关题目
