题目内容
如图所示,MN是竖直放置的长L=0.5m的平面镜,观察者在A处观察,有一小球从某处自由下落,小球下落的轨迹与平面镜相距d=0.25m,观察者的眼睛到镜面的距离s=0.5m,小球从静止开始下落0.275s后,观察者才能在镜中看到小球的像,求观察者在镜中看到小球像的时间△t为多少?(取g=10m/s2)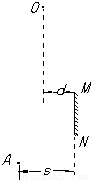
【答案】分析:本题的关键是根据“视物原理”和平面镜作图法做出人眼在A点能看到范围,即物体从O点下落过程中,人眼能看到的区域是BC,然后再根据自由落体规律并结合几何知识,即可求解△t.
解答:解:根据平面镜作图方法做出光路图如图所示,小球在下落过程中从B到C过程人眼睛才能看到,由几何知识应有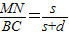 =
= ,所以BC=
,所以BC=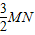 =
=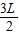 =0.75m,
=0.75m,
再由自由落体规律可得:OB=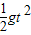 =
=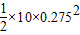 m=0.378m,所以OC=OB+BC=1.128m
m=0.378m,所以OC=OB+BC=1.128m
设观察者能在镜中看到小球像的时间为△t,则OC=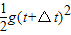 =
=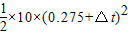 ,代入数据解得△t=0.2s
,代入数据解得△t=0.2s
故观察者在镜中看到小球像的时间△t为0.2s.
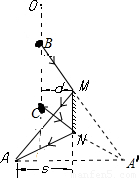
点评:掌握平面镜作图法以及光路可逆原理,把人眼看做“点光源”,则平面镜能照亮的区域即为能看到的区域.
解答:解:根据平面镜作图方法做出光路图如图所示,小球在下落过程中从B到C过程人眼睛才能看到,由几何知识应有
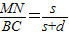 =
= ,所以BC=
,所以BC=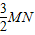 =
=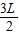 =0.75m,
=0.75m,再由自由落体规律可得:OB=
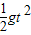 =
=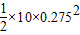 m=0.378m,所以OC=OB+BC=1.128m
m=0.378m,所以OC=OB+BC=1.128m设观察者能在镜中看到小球像的时间为△t,则OC=
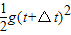 =
=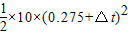 ,代入数据解得△t=0.2s
,代入数据解得△t=0.2s故观察者在镜中看到小球像的时间△t为0.2s.

点评:掌握平面镜作图法以及光路可逆原理,把人眼看做“点光源”,则平面镜能照亮的区域即为能看到的区域.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图所示,MN是竖直放置的长L=0.5m的平面镜,观察者在A处观察,有一小球从某处自由下落,小球下落的轨迹与平面镜相距d=0.25m,观察者的眼睛到镜面的距离s=0.5m,小球从静止开始下落0.275s后,观察者才能在镜中看到小球的像,求观察者在镜中看到小球像的时间△t为多少?(取g=10m/s2)
如图所示,MN是竖直放置的长L=0.5m的平面镜,观察者在A处观察,有一小球从某处自由下落,小球下落的轨迹与平面镜相距d=0.25m,观察者的眼睛到镜面的距离s=0.5m,小球从静止开始下落0.275s后,观察者才能在镜中看到小球的像,求观察者在镜中看到小球像的时间△t为多少?(取g=10m/s2)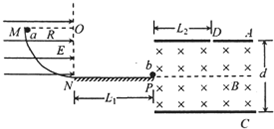 (2012?绵阳模拟)如图所示,MN是竖直平面内的1/4圆弧轨道,绝缘光滑,半径R=lm.轨道区域存在E=4N/C、方向水平向右的匀强电场.长L1=5m的绝缘粗糖水平轨道NP与圆弧轨道相切于N点.质量ma=100g、电荷量qa=+1C的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,mb=50g,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间.已知小球a恰能从C板的右端飞出,速度为vac=
(2012?绵阳模拟)如图所示,MN是竖直平面内的1/4圆弧轨道,绝缘光滑,半径R=lm.轨道区域存在E=4N/C、方向水平向右的匀强电场.长L1=5m的绝缘粗糖水平轨道NP与圆弧轨道相切于N点.质量ma=100g、电荷量qa=+1C的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,mb=50g,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间.已知小球a恰能从C板的右端飞出,速度为vac=
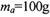 、电荷量
、电荷量 的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,
的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,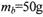 ,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为
,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为 ,小球b打在A板的D孔,D孔距板基端
,小球b打在A板的D孔,D孔距板基端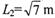 ,A,C板间电势差
,A,C板间电势差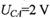 ,A,C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求:
,A,C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求: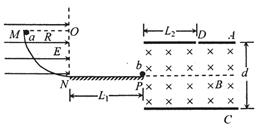
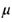 是多大?
是多大?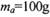 、电荷量
、电荷量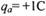 的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,
的金属小球a从M点由静止开始沿圆弧轨道下滑,进人NP轨道随线运动,与放在随右端的金属小球b发生正碰,b与a等大,不带电,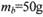 ,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为
,b与a碰后均分电荷量,然后都沿水平放置的A、C板间的中线进入两板之间。已知小球a恰能从C板的右端飞出,速度为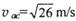 ,小球b打在A板的D孔,D孔距板基端
,小球b打在A板的D孔,D孔距板基端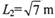 ,A,C板间电势差
,A,C板间电势差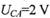 ,A, C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求:
,A, C板间有匀强磁场,磁感应强度5=0.2T,板间距离d=2m,电场和磁编仅存在于两板之间。g=10m/s2求:
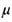 是多大?
是多大?