Question

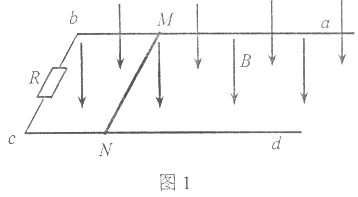
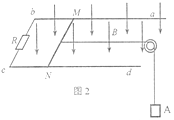
【题目】如图所示，有一光滑、不计电阻且足够长的平行金属导轨，间距L＝0.5m，导轨所在的平面与水平面的倾角为37°，导轨空间内存在垂直导轨平面的匀强磁场。现将一质量m＝0.2kg、电阻R＝2Ω的金属杆水平靠在导轨处，与导轨接触良好。（g＝10m/s2，sin37°＝0.6，cos37°＝0.8）

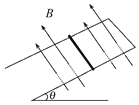
（1）若磁感应强度随时间变化满足B＝4+0.5t（T），金属杆由距导轨顶部1m处释放，求至少经过多长时间释放，会获得沿斜面向上的加速度。

（2）若磁感应强度随时间变化满足 （T），t＝0时刻金属杆从离导轨顶端s0＝1m处静止释放，同时对金属杆施加一个外力，使金属杆沿导轨下滑且没有感应电流产生，求金属杆下滑5m所用的时间。

（3）若匀强磁场大小为定值，对金属杆施加一个平行于导轨向下的外力F，其大小为F＝（v+0.8）N，其中v为金属杆运动的速度，使金属杆以恒定的加速度a＝10m/s2沿导轨向下做匀加速运动，求匀强磁场磁感应强度B的大小。

Answer 1

【答案】（1）30.4s; （2）s； （3） T。

【解析】

(1)设金属杆长为L，距离导轨顶部为x，经过ts后，金属杆有沿着导轨向上的加速度，此时安培力等于重力沿导轨的分力，则：

FA＝mgsinθ，

，

其中：

，

所以：

，

解得：

t＝30.4s。

（2）由金属杆与导轨组成的闭合电路中，磁通量保持不变，经过ts的位移为s，则：

B1Ls0＝B2L（s+s0），

金属杆做初速度为零的匀加速直线运动，

s＝5m，

代入数据解得：

（3）对金属杆由牛顿第二定律：

，

其中：

解得：

，

代入数据得：

，

所以，

，

解得： 。