题目内容
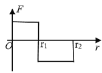
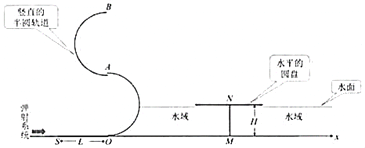
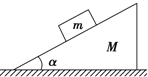
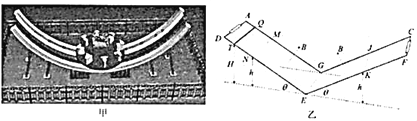
【题目】如图所示,甲图是游乐场的“空中摩托”设备示意图,为了缩短项目收尾时的制动时间,某兴趣小组设计了乙图所示的简化模型。平行光滑金属导轨AG和DE、GC和EF的间距均为L,与水平面夹角均为θ,在最低点G、E平滑连接且对称固定于水平地面上。导轨的两端AD、CF间均接有阻值为R的电阻。在导轨的NMGE和GEKJ两个矩形区域内存在着匀强磁场,磁感应强度大小均为B,方向分别垂直于两轨道平面向上;区域边界MN和JK的离地高度均为h。现将“空中摩托”简化为电阻为r,质量为m,长为L的导体棒QT,它垂直导轨由离地为H的高度处从静止释放。若导体棒QT第一次到达GE时速度大小为v,第一次到达JK时速度恰好为0.假设整个过程QT均垂直于导轨且与导轨接触良好,不计导轨电阻,不计空气阻力和摩擦,重力加速度为g。求:
(1)导体棒QT第一次经过MN时它两端的电压大小;
(2)导体棒QT从静止释放后到最终状态的整个过程中它的发热量;
(3)导体棒QT从静止释放后到它第一次到达JK的时间;
(4)试判断题中的物理量R和B对制动时间是否有影响;若有影响,请分析如何调整该变量,可以缩短制动时间(即相同情况下在更短的时间内停下来)?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)物理量R和B对制动时间有影响。应减小R,增大B,来缩短制动时间
;(4)物理量R和B对制动时间有影响。应减小R,增大B,来缩短制动时间
【解析】
先根据机械能守恒定律求出导体棒QT第一次经过MN时的速度。由E=BLv求出QT产生的感应电动势,由电压的分配关系求QT两端的电压;由于电磁感应产生电流,从而使QT的重力势能mgH全部转化为焦耳热,结合电路的结构求导体棒QT整个过程中的发热量;对导体棒下滑和上滑的过程,分别运用动量定理列式,可求得导体棒QT从静止释放后到它第一次到达JK的时间;根据上题的结果,分析物理量R和B对制动时间是否有影响。
(1)导体棒QT从静止释放到第一次经过MN的过程,
由机械能守恒定律得:![]()
解得:![]()
导体棒QT第一次经过MN时产生的感应电动势为:![]()
导体棒QT第一次经过MN时它两端的电压为:![]()
(2)由于电磁感应产生电流,从而使QT的重力势能mgH全部转化为焦耳热,考虑到电路结构,故QT上的发热量为:![]()
(3)下滑阶段,由动量定理得:mgsinθt1﹣BI1Lt1=mv,
上滑阶段,由动量定理得:﹣mgsinθt2﹣BI2Lt2=0﹣mv
又 BI1Lt1′=BLq1,q1是下滑阶段通过QT的电荷量
BI2Lt2′=BLq2,q2是下滑阶段通过QT的电荷量
根据![]() 知:q1=q2
知:q1=q2
所以解得:![]()
(4)物理量R和B对制动时间有影响。R越小,B越大,QT下滑过程受到的安培力平均值越大,产生的焦耳热越大,到达GE时速度v越小,由上式知t越短,所以应减小R,增大B,来缩短制动时间。

 阅读快车系列答案
阅读快车系列答案