题目内容
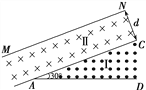
【题目】如图1所示，固定于水平面的U形导线框abcd处于竖直向下、磁感应强度为B的匀强磁场中，导线框两平行导轨间距为l，左端接一电阻R。一质量为m、电阻为r的导体棒MN垂直导线框放置。
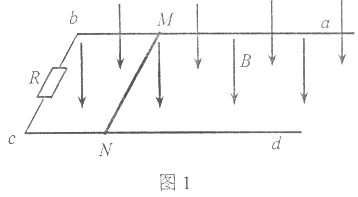
（1）若导体棒沿导线框以速度v向右做匀速运动。请根据法拉第电磁感应定律E=
，推导金属棒MN中的感应电动势E。
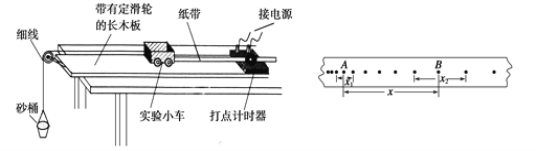
（2）若将导体棒与重物A用不可伸长的细线相连，细线绕过定滑轮，导体棒与滑轮之间的细线保持水平，如图2所示。静止释放重物，重物将通过细线拉动导体棒开始运动，运动过程中导体棒不会与定滑轮发生碰撞。若重物A的质量也为m，不计细线的质量以及一切摩擦。
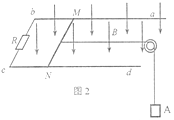
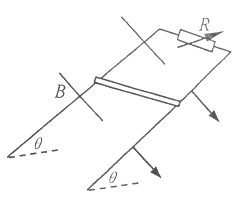
i）在图3中定性画出导体棒MN的速度v随时间t变化的图象；
ii）当重物从静止开始下落，下落的高度为h时，重物的速度为v，此时导体棒的速度还没有达到稳定，在此过程中，求：
a. 电阻R上产生的焦耳热；
b. 导体棒的运动时间。
【答案】（1）E=BLv
（2）i）如图所示；
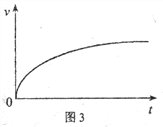
ii）a. 
b. 
【解析】（1）设经过时间t，金属棒运动的距离为x=vt；
根据法拉第电磁感应定律： 
（2）（i）某时刻金属棒产生的电动势E=BLv；
感应电流： 
所受的安培力： 
加速度
即： 
，则随速度的增加，加速度逐渐减小，故v-t图像如图；
（ⅱ）a.由能量关系可知： 
解得： 
b.对两棒的系统，由动量定理可得： 
解得： 
练习册系列答案
相关题目
