题目内容
14.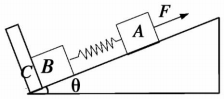 如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )
如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )| A. | 弹簧的劲度系数k=$\frac{{m}_{B}gsinθ}{d}$ | |
| B. | 弹簧的劲度系数k=$\frac{{m}_{A}gsinθ}{d}$ | |
| C. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$ | |
| D. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}+{m}_{B}}$ |
分析 先由胡克定律求出未施力F时弹簧的压缩量,再求出物块B刚要离开C时弹簧的伸长量,由几何知识求出物块A的位移大小,即可求得弹簧的劲度系数.当B刚离开C时,弹簧的弹力等于B的重力沿斜面下的分力.根据牛顿第二定律求出物块A的加速度大小;
解答 解:A、当未施加外力时,对A受力分析可知:mAgsinθ=kx1
当施加上外力后,B刚好脱离时,对B受力分析可知:mBgsinθ=kx2
x1+x2=d
联立解得$k=\frac{({m}_{A}+{m}_{B})gsinθ}{d}$,故AB错误;
C、对物体A受力分析,根据牛顿第二定律可知F-mAgsinθ-F弹=mAa
F弹=mBgsinθ
联立解得a=$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$,故C正确,D错误
故选:C
点评 含有弹簧的问题,往往要研究弹簧的状态,分析物块的位移与弹簧压缩量和伸长量的关系是常用思路.

练习册系列答案
相关题目
4.甲、乙两颗圆球形行星半径分别为R和2R,质量分别为M和2M,若不考虑行星自转的影响,下述判断正确的是( )
| A. | 质量相同的物体在甲、乙行星表面所受万有引力大小F甲>F乙 | |
| B. | 两颗行星表面的重力加速度g甲>g乙 | |
| C. | 两颗行星的卫星的最大环绕速度v甲>v乙 | |
| D. | 两颗行星的卫星的最大环绕速度v甲<v乙 |
5. 如图所示是一定质量的O2在0℃和100℃时分子数与分子速率的图象.从图象中可以得到的正确结论是( )
如图所示是一定质量的O2在0℃和100℃时分子数与分子速率的图象.从图象中可以得到的正确结论是( )
 如图所示是一定质量的O2在0℃和100℃时分子数与分子速率的图象.从图象中可以得到的正确结论是( )
如图所示是一定质量的O2在0℃和100℃时分子数与分子速率的图象.从图象中可以得到的正确结论是( )| A. | 曲线甲是O2在0℃时的图象 | |
| B. | 无论是0℃还是100℃,中等速率的氧气分子占大多数 | |
| C. | 存在某一速率,0℃和100℃时氧气分子数相等 | |
| D. | 100℃时O2分子的速率都大于0℃时O2分子的速率 | |
| E. | 曲线甲对应的O2分子的总动能大于曲线乙对应的O2分子的总动能 |
9. 如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )
如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )
 如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )
如图所示,一战斗机在距地面高度一定的空中,由东向西沿水平方向匀速飞行,发现地面目标P后,开始瞄准并投掷炸弹.若炸弹恰好击中目标P,假设投弹后飞机仍以原速度水平匀速飞行(空气阻力不计),则( )| A. | 飞机投弹时在P点的正上方 | |
| B. | 炸弹落在P点时,飞机在P点的正上方 | |
| C. | 飞机飞行速度越大,投弹时飞机到P点的距离应越大 | |
| D. | 无论飞机飞行速度多大,从投弹到击中目标经历的时间是一定的 |
19.下列说法正确的是( )
| A. | 所有的固体都有固定的熔点,物理性质各向异性 | |
| B. | 气体从外界吸收热量,其内能不一定增加 | |
| C. | 布朗运动就是液体分子的无规则运动 | |
| D. | 荷叶上的水珠之所以表现为球状,是因为液体表面张力作用的结果 | |
| E. | 当两个分子处于平衡状态时,分子势能最小 |
3.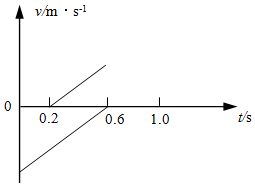 小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )
小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )
 小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )
小球a从地面以一定的速度竖直向上抛出,经过一段时间后小球b从a的上方一定高度处由静止释放,最终两小球(均视为质点)同时落地.从a拋出的时刻开始计时,两小球在0~0.6s内的v-t图象如图所示.不计空气阻力,重力加速度g=10m/s2,下列判断正确的是( )| A. | 小球a抛出时的速率为6m/s | |
| B. | 小球b落地时的速率为8m/s | |
| C. | 从t=0时刻开始,a、b速率之差的绝对值先变小后变大 | |
| D. | t=0.6s 时,a、b间距为2.4m |
1.对向心力的两个公式①F=mω2r和②F=m$\frac{{v}^{2}}{r}$的理解,下列说法中正确的是( )
| A. | 两个公式都表明在其他条件不变时,做匀速圆周运动的物体所需向心力与物体质量m成正比 | |
| B. | 公式①表明向心力跟半径r成正比 | |
| C. | 公式②表明向心力跟半径r成反比 | |
| D. | 公式①表明在角速度不变的情况下,向心力跟圆半径r成正比 |
 如图,以竖直向上为y轴正方向建立直角坐标系;该真空中存在方向沿x轴正向、场强为E的匀强电场和方向垂直xoy平面向外、磁感应强度为B的匀强磁场;原点O处的离子源连续不断地发射速度大小和方向一定、质量为m、电荷量为-q(q>0)的粒子束,粒子恰能在xoy平面内做直线运动,重力加速度为g,不计粒子间的相互作用;
如图,以竖直向上为y轴正方向建立直角坐标系;该真空中存在方向沿x轴正向、场强为E的匀强电场和方向垂直xoy平面向外、磁感应强度为B的匀强磁场;原点O处的离子源连续不断地发射速度大小和方向一定、质量为m、电荷量为-q(q>0)的粒子束,粒子恰能在xoy平面内做直线运动,重力加速度为g,不计粒子间的相互作用;