题目内容
4.甲、乙两颗圆球形行星半径分别为R和2R,质量分别为M和2M,若不考虑行星自转的影响,下述判断正确的是( )| A. | 质量相同的物体在甲、乙行星表面所受万有引力大小F甲>F乙 | |
| B. | 两颗行星表面的重力加速度g甲>g乙 | |
| C. | 两颗行星的卫星的最大环绕速度v甲>v乙 | |
| D. | 两颗行星的卫星的最大环绕速度v甲<v乙 |
分析 根据万有引力定律分析万有引力的大小.由重力等于万有引力,列式得到行星表面的重力加速度的表达式,再比较大小.抓住卫星做圆周运动的向心力由万有引力提供,列式分析环绕速度的大小.
解答 解:A、根据万有引力定律得:$\frac{{F}_{甲}}{{F}_{乙}}$=$\frac{G\frac{Mm}{{R}^{2}}}{G\frac{2Mm}{(2R)^{2}}}$=2,所以F甲>F乙.故A正确.
B、不考虑行星自转的影响,行星表面的物体受到的重力等于万有引力,则有:G$\frac{Mm}{{R}^{2}}$=mg,得:g=$\frac{GM}{{R}^{2}}$
所以得:$\frac{{g}_{甲}}{{g}_{乙}}$=$\frac{\frac{GM}{{R}^{2}}}{\frac{G•2M}{(2R)^{2}}}$=2,所以g甲>g乙.故B正确.
CD、设最大环绕速度为v.由G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,可得:v=$\sqrt{\frac{GM}{r}}$,(r是行星的半径),则得:$\frac{{v}_{甲}}{{v}_{乙}}$=$\frac{\sqrt{\frac{GM}{R}}}{\sqrt{\frac{G•2M}{2R}}}$=1,所以v甲=v乙.故CD错误.
故选:AB
点评 抓住万有引力等于向心力和万有引力等于重力列式,这是解决本题的关键,要注意中心天体的质量是不同的.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14. 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等.实线为一带负电的粒子,仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知,下列说法中正确的是( )| A. | 三个等势面中,c点的电势最高 | |
| B. | 粒子在P点的加速度方向沿着等势面a的切线方向 | |
| C. | 对于P、Q两点,带电粒子通过P点时电势能较大 | |
| D. | 由于不知道带电粒子运动的方向,无法比较P、Q两点的动能大小 |
12.开发更为安全、清洁的能源是人类不懈的追求.关于核反应${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n,下列说法正确的是( )
| A. | 该核反应属于重核的裂变 | |
| B. | 该核反应属于轻核的聚变 | |
| C. | 该核反应过程没有质量亏损 | |
| D. | 目前核电站利用的就是该核反应所释放的能量 |
19.氢原子能级如图,当氢原子n=3跃迁到n=2的能级时,辐射光的波长为656nm.以下判断正确的是( ) 

| A. | 氢原子从n=2跃迁到n=1的能级时,辐射光的波长大于656nm | |
| B. | 用波长为325nm的光照射,可使氢原子从n=1跃迁到n=2能级 | |
| C. | 一群处于n=3能级上的氢原子向低能级跃迁时最多产生4种谱线 | |
| D. | 用波长为633nm的光照射,不能使氢原子从n=2跃迁到n=3的能级 |
16. 如图所示是氢原子的能级图,现有一群处于n=4能级上的氢原子,它们在跃迁回到n=1能级的过程中,可能辐射出N种不同频率的光子.辐射出的光子照射某种金属,能产生的光电子最大初动能是Ek,已知该金属的逸出功是4.20eV,则( )
如图所示是氢原子的能级图,现有一群处于n=4能级上的氢原子,它们在跃迁回到n=1能级的过程中,可能辐射出N种不同频率的光子.辐射出的光子照射某种金属,能产生的光电子最大初动能是Ek,已知该金属的逸出功是4.20eV,则( )
 如图所示是氢原子的能级图,现有一群处于n=4能级上的氢原子,它们在跃迁回到n=1能级的过程中,可能辐射出N种不同频率的光子.辐射出的光子照射某种金属,能产生的光电子最大初动能是Ek,已知该金属的逸出功是4.20eV,则( )
如图所示是氢原子的能级图,现有一群处于n=4能级上的氢原子,它们在跃迁回到n=1能级的过程中,可能辐射出N种不同频率的光子.辐射出的光子照射某种金属,能产生的光电子最大初动能是Ek,已知该金属的逸出功是4.20eV,则( )| A. | N=3 | B. | N=6 | C. | Ek=8.55 eV | D. | Ek=9.40 eV |
13.关于α、β、γ三种射线,下列说法正确的是( )
| A. | α射线是原子核自发放射出的氦核 | |
| B. | β射线是原子核外电子电离形成的电子流 | |
| C. | γ射线的穿透能力最强 | |
| D. | γ射线的电离本领最强 |
14.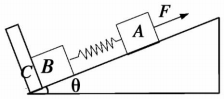 如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )
如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )
 如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )
如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )| A. | 弹簧的劲度系数k=$\frac{{m}_{B}gsinθ}{d}$ | |
| B. | 弹簧的劲度系数k=$\frac{{m}_{A}gsinθ}{d}$ | |
| C. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$ | |
| D. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}+{m}_{B}}$ |
 某同学设计了一个探究平抛运动特点的家庭实验装置,如图所示.在水平桌面上放置一个斜面,每次都让钢球从斜面上同一位置静止释放滚下,滚过桌面后钢球便做平抛运动.在钢球抛出后经过的地方水平放置一块木板(还有一个用来调节木板高度的支架,图中未画出),板上放一张白纸,白纸上有复写纸,这样便能记录钢球在白纸上的落点.桌子边缘钢球经过的地方挂一条铅垂线.已知平抛运动在竖直方向上的运动规律与自由落体运动相同,在此前提下探究钢球水平分速度的特点.
某同学设计了一个探究平抛运动特点的家庭实验装置,如图所示.在水平桌面上放置一个斜面,每次都让钢球从斜面上同一位置静止释放滚下,滚过桌面后钢球便做平抛运动.在钢球抛出后经过的地方水平放置一块木板(还有一个用来调节木板高度的支架,图中未画出),板上放一张白纸,白纸上有复写纸,这样便能记录钢球在白纸上的落点.桌子边缘钢球经过的地方挂一条铅垂线.已知平抛运动在竖直方向上的运动规律与自由落体运动相同,在此前提下探究钢球水平分速度的特点.