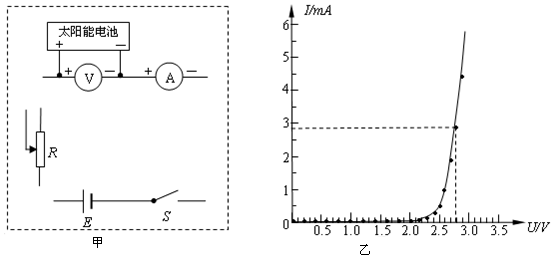
题目内容
2. 如图,以竖直向上为y轴正方向建立直角坐标系;该真空中存在方向沿x轴正向、场强为E的匀强电场和方向垂直xoy平面向外、磁感应强度为B的匀强磁场;原点O处的离子源连续不断地发射速度大小和方向一定、质量为m、电荷量为-q(q>0)的粒子束,粒子恰能在xoy平面内做直线运动,重力加速度为g,不计粒子间的相互作用;
如图,以竖直向上为y轴正方向建立直角坐标系;该真空中存在方向沿x轴正向、场强为E的匀强电场和方向垂直xoy平面向外、磁感应强度为B的匀强磁场;原点O处的离子源连续不断地发射速度大小和方向一定、质量为m、电荷量为-q(q>0)的粒子束,粒子恰能在xoy平面内做直线运动,重力加速度为g,不计粒子间的相互作用;(1)求粒子运动到距x轴为h所用的时间;
(2)若在粒子束运动过程中,突然将电场变为竖直向下、场强大小变为E′=$\frac{mg}{q}$,求从O点射出的所有粒子第一次打在x轴上的坐标范围(不考虑电场变化产生的影响);
(3)若保持EB初始状态不变,仅将粒子束的初速度变为原来的2倍,求运动过程中,粒子速度大小等于初速度λ倍(0<λ<2)的点所在的直线方程.
分析 (1)根据粒子做直线运动求得粒子受力情况,进而根据洛伦兹力求得速度;再由速度求得y方向的分量,进而求得运动时间;
(2)分析改变电场后粒子的受力情况及运动情况,然后讨论在粒子运动的不同位置改变电场得到的结果,进而求得坐标范围;
(3)由速度改变得到粒子运动状态改变,再根据动能定理求得x,y的关系,得到直线方程.
解答 解:(1)粒子恰能在xoy平面内做直线运动,则粒子在垂直速度方向上所受合外力一定为零;
又有电场力和重力为恒力,其在垂直速度方向上的分量不变,而要保证该方向上合外力为零,则洛伦兹力大小不变;
因为洛伦兹力F洛=Bvq,所以,速度大小不变,即粒子做匀速直线运动,重力、电场力和磁场力三个力的合力为零;
设重力与电场力合力与-y轴夹角为θ,粒子受力如图所示,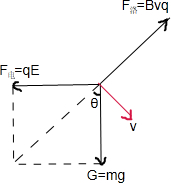 ,
,
所以,(Bvq)2=(qE)2+(mg)2,所以,$v=\frac{\sqrt{(qE)^{2}+(mg)^{2}}}{Bq}$,
则v在y方向上分量大小${v}_{y}=v•sinθ=v•\frac{qE}{Bvq}=\frac{E}{B}$,
因为粒子做匀速直线运动,根据运动的分解可得,粒子运动到距x轴为h所用的时间$t=\frac{h}{{v}_{y}}=\frac{Bh}{E}$;
(2)若在粒子束运动过程中,突然将电场变为竖直向下、场强大小变为E′=$\frac{mg}{q}$,则电场力${{F}_{电}}^{'}=q{E}^{'}=mg$,电场力方向竖直向上;
所以,粒子所受合外力就是洛伦兹力,则有,洛伦兹力作向心力,即$Bvq=\frac{m{v}^{2}}{R}$,
所以,$R=\frac{mv}{Bq}=\frac{m\sqrt{(qE)^{2}+(mg)^{2}}}{{B}^{2}{q}^{2}}$;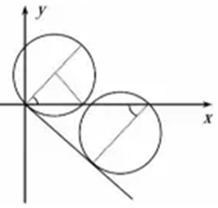
如上图所示,由几何关系可知,当粒子在O点是就改变电场,第一次打在x轴上的横坐标最小,${x}_{1}=2Rsinθ=2×\frac{m\sqrt{(qE)^{2}+(mg)^{2}}}{{B}^{2}{q}^{2}}×\frac{qE}{\sqrt{(qE)^{2}+(mg)^{2}}}$=$\frac{2mE}{{B}^{2}q}$;
当改变电场时粒子所在处与粒子第一次打在x轴上的位置之间的距离为2R时,第一次打在x轴上的横坐标最大,${x}_{2}=\frac{2R}{sinθ}=\frac{\frac{2m\sqrt{(qE)^{2}+(mg)^{2}}}{{B}^{2}{q}^{2}}}{\frac{qE}{\sqrt{(qE)^{2}+(mg)^{2}}}}=\frac{2m[(qE)^{2}+(mg)^{2}]}{{B}^{2}{q}^{3}E}$;
所以,从O点射出的所有粒子第一次打在x轴上的坐标范围为x1≤x≤x2,即$\frac{2mE}{{B}^{2}q}≤x≤\frac{2m[(qE)^{2}+(mg)^{2}]}{{B}^{2}{q}^{3}E}$;
(3)粒子束的初速度变为原来的2倍,则粒子不能做匀速直线运动,粒子必发生偏转,则洛伦兹力不做功,电场力和重力对粒子所做的总功必不为零;
那么设离子运动到位置坐标(x,y)满足速率v′为初速度大小v0′的λ倍,则根据动能定理:$-qEx-mgy=\frac{1}{2}mv{′}^{2}-\frac{1}{2}m{v}_{0}{′}^{2}$=$\frac{1}{2}m({λ}^{2}-1){v}_{0}{′}^{2}$;
因为粒子束的初速度变为原来的2倍,即v0′=2v,所以,-qEx-mgy=2m(λ2-1)v2;
所以,$-qEx-mgy=2m({λ}^{2}-1)•\frac{(qE)^{2}+(mg)^{2}}{{B}^{2}{q}^{2}}$;
所以,$y=-\frac{qE}{mg}x-\frac{2({λ}^{2}-1)[(qE)^{2}+(mg)^{2}]}{{B}^{2}{q}^{2}g}$.
答:(1)粒子运动到距x轴为h所用的时间为$\frac{Bh}{E}$;
(2)若在粒子束运动过程中,突然将电场变为竖直向下、场强大小变为E′=$\frac{mg}{q}$,则从O点射出的所有粒子第一次打在x轴上的坐标范围(不考虑电场变化产生的影响)为$[\frac{2mE}{{B}^{2}q},\frac{2m[(qE)^{2}+(mg)^{2}]}{{B}^{2}{q}^{3}E}]$;
(3)若保持E、B初始状态不变,仅将粒子束的初速度变为原来的2倍,则运动过程中,粒子速度大小等于初速度λ倍(0<λ<2)的点所在的直线方程为$y=-\frac{qE}{mg}x-\frac{2({λ}^{2}-1)[(qE)^{2}+(mg)^{2}]}{{B}^{2}{q}^{2}g}$.
点评 求物体运动问题时,改变条件后的问题求解需要对条件改变引起的运动变化进行分析,从变化的地方开始进行求解.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 该核反应属于重核的裂变 | |
| B. | 该核反应属于轻核的聚变 | |
| C. | 该核反应过程没有质量亏损 | |
| D. | 目前核电站利用的就是该核反应所释放的能量 |
| A. | α射线是原子核自发放射出的氦核 | |
| B. | β射线是原子核外电子电离形成的电子流 | |
| C. | γ射线的穿透能力最强 | |
| D. | γ射线的电离本领最强 |
| A. | 悬浮在液体中的固体微粒越小,布朗运动越明显 | |
| B. | 液晶其光学性质与某些晶体相似,具有各向异性 | |
| C. | 一定质量的理想气体从外界吸收热量,其内能一定增加 | |
| D. | 单位时间内气体分子对容器壁单位面积上碰撞次数减少,气体压强一定减少 | |
| E. | 雨后叶子表面上的小水珠接近球形主要是液体表面张力作用的结果 |
 1772年,法籍意大利数学家拉格朗日在论文《三体问题》指出:两个质量相差悬殊的天体(如太阳和地球)所在同一平面上有5个特殊点,如图中的L1、L2、L3、L4、L5所示,人们称为拉格朗日点.若飞行器位于这些点上,会在太阳与地球共同引力作用下,可以几乎不消耗燃料而保持与地球同步绕太阳做圆周运动.由于这五个点的特殊性,已经成为各个航天大国深空探测所争夺的地方.2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里的拉格朗日L2点,下列说法正确的是( )
1772年,法籍意大利数学家拉格朗日在论文《三体问题》指出:两个质量相差悬殊的天体(如太阳和地球)所在同一平面上有5个特殊点,如图中的L1、L2、L3、L4、L5所示,人们称为拉格朗日点.若飞行器位于这些点上,会在太阳与地球共同引力作用下,可以几乎不消耗燃料而保持与地球同步绕太阳做圆周运动.由于这五个点的特殊性,已经成为各个航天大国深空探测所争夺的地方.2012年8月25日23时27分,经过77天的飞行,“嫦娥二号”在世界上首次实现从月球轨道出发,受控准确进入距离地球约150万公里的拉格朗日L2点,下列说法正确的是( )| A. | “嫦娥二号”绕太阳运动周期和地球自转周期相等 | |
| B. | “嫦娥二号”在L2点处于平衡状态 | |
| C. | “嫦娥二号”绕太阳运动的向心加速度大于地球绕太阳运动的向心加速度 | |
| D. | “嫦娥二号”在L2处所受太阳和地球引力的合力比在L1处小 |
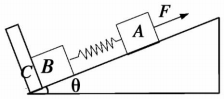 如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )
如图所示,倾角为θ的光滑斜面上静止放置两个用劲度系数为k的轻弹簧连接的物块A、B,它们的质量分别为mA、mB,C固定为挡板,系统保持静止.现在物块A上施加一个沿斜面向上的恒力F,当物块B即将离开C时,物块A的运动距离为d,则( )| A. | 弹簧的劲度系数k=$\frac{{m}_{B}gsinθ}{d}$ | |
| B. | 弹簧的劲度系数k=$\frac{{m}_{A}gsinθ}{d}$ | |
| C. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}}$ | |
| D. | 物块B刚离开C时物块A的加速度为$\frac{F-({m}_{A}+{m}_{B})gsinθ}{{m}_{A}+{m}_{B}}$ |
| A. | 可能做匀减速直线运动,加速度大小可能是8m/s2 | |
| B. | 可能做匀加速直线运动,加速度大小可能是4m/s2 | |
| C. | 可能做类平抛运动,加速度大小可能10m/s2 | |
| D. | 速度可能先减小后增大 |
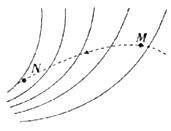 如图所示,实线为某电场的电场线,虚线为某一带负电粒子只在电场力作用下的运动轨迹,M、N为运动轨迹上两点,下列说法中正确的是( )
如图所示,实线为某电场的电场线,虚线为某一带负电粒子只在电场力作用下的运动轨迹,M、N为运动轨迹上两点,下列说法中正确的是( )| A. | 该粒子在M点的动能一定小于在N点的动能 | |
| B. | 该粒子在M点的电势能一定小于在N点的电势能 | |
| C. | M点的电势一定高于N点的电势 | |
| D. | 该粒子在M点的加速度一定大于在N点的加速度 |