Question

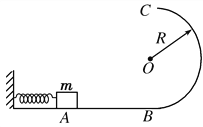
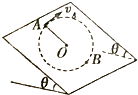
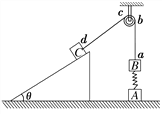
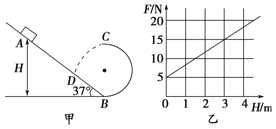
【题目】如图甲所示，一竖直平面内的轨道由粗糙斜面AB和光滑半圆轨道BC组成，斜面底端通过一小段圆弧（图中未画出，长度可不计）与轨道相切于B点．斜面的倾角为37°，半圆轨道半径为1m，B是圆轨道的最低点，C为最高点．将一小物块置于轨道AB上离地面高为H处由静止下滑，用力传感器测出其经过B点时对轨道的压力F，改变H的大小，可测出相应的F的大小，F随H的变化规律如图乙所示．物块在某次运动时，由H=8.4m处释放，通过C后，又落回到斜面上D点．（已知sin37°=0.6， cos37°=0.8，g取10m/s2）求：

（1）物块的质量及物块与斜面间的动摩擦因数．

（2）物块落到D点时的速度大小．

Answer 1

【答案】（1）物块的质量为0.5kg，物块与斜面间的动摩擦因数为0.5．

　（2）物块落到D点时的速度大小为m/s．

【解析】（1）物块从斜面上A点滑到B点的过程中，由动能定理得：

①

物块在B点满足：F－mg＝m ②

由①②可得： ③

由图象可知：H＝0时，F＝5 N；H＝3 m时，F＝15 N

代入③解得：m＝0.5 kg，μ＝0.5.

（2）物块从A到C由动能定理得：mg(H－2R)－μmgHcot 37°＝ ④

物块从C到D做平抛运动，下落高度h＝gt2 ⑤ 水平位移x＝vCt ⑥

由几何关系知：tan 37°＝ ⑦

由④⑤⑥⑦可得：t＝0.4 s

物块到D点时的速度的大小：