Question

【题目】如图所示，在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上；B、C两物体通过细线绕过轻质定滑轮相连，C放在固定的光滑斜面上。用手拿住C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行。已知A、B的质量均为m，斜面倾角为θ=37°，重力加速度为g，滑轮的质量和摩擦不计，开始时整个系统处于静止状态。C释放后沿斜面下滑，当A刚要离开地面时，B的速度最大。(sin 37°=0.6，cos 37°=0.8)求：

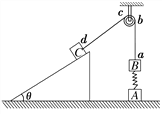
（1）从开始到A刚要离开地面的过程中，C沿斜面下滑的距离；

（2）C的质量；

（3）A刚离开地面时，C的动能。

Answer 1

【答案】（1）（2）（3）

【解析】试题分析：由胡克定律及共点力的平衡条件可知物体下滑的距离；对B及C分别受力分析由共点力的平衡条件可求得C的质量；对BC由动能定理可求得拉力所做的功．

（1）设开始时弹簧压缩的长度为，由题意有：

设当A刚刚离开地面时，弹簧的伸长量为，有

当A刚离开地面时，B上升的距离即C沿斜面下滑的距离为。

（2）A刚离开地面时，以B为研究对象，B受到重力mg、弹簧的弹力kxA，细线的拉力FT三个力的作用，设B的加速度为a，根据牛顿第二定律，对B有：

对C有：

当B获得最大速度时，有，解得。

（3）根据动能定理得：

对C：

对B：

其中弹簧弹力先做正功后做负功，且其压缩量与伸长量相等，故总功为零，

B、C的速度大小相等，故其动能大小之比为其质量大小之比，即

解得。