题目内容
【题目】如图所示，在倾角为θ的光滑斜面上，有一长为l的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在斜面上做完整的圆周运动，则（ ）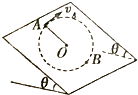
A.小球通过最高点A时的速度vA= 
B.小球通过最高点A时的速度vA= 
C.小球通过最高点A时，细线对小球的拉力T=0
D.小球通过最高点A时，细线对小球的拉力T=mgsinθ
【答案】A,C
【解析】解：小球在斜面上做圆周运动的等效重力G′=mgsinθ，恰好通过最高点A时只有等效重力提供向心力，故此时有T=0，
根据牛顿第二定律得：mgsinθ=m 
，所以vA= 
，故AC正确．
故选：AC
【考点精析】解答此题的关键在于理解向心力的相关知识，掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
