��Ŀ����
����Ŀ����ͼ��ʾ���⻬ˮƽ��AB����ֱ���ڵİ�Բ�ι����B�����У���Բ�ι���İ뾶ΪR��һ������Ϊm�����彫����ѹ����A����ɾ�ֹ�ͷţ��ڵ���������������ijһ���ҵ��ٶȺ����뵯�ɣ���������B���������˲��Թ����ѹ��Ϊ��������8����֮�������˶�ǡ�ܵ�����ߵ�C(���ƿ�������)������
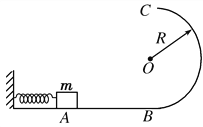
��1��������A��ʱ���ɵĵ������ܣ�
��2�������B���˶���C��Ĺ����в��������ܡ�
���𰸡���1��![]() ��2��mgR
��2��mgR
�������������������1����������B����ٶ�ΪvB�����ܵ���ΪFNB��
����FNB��mg=m![]() ����FNB=8mg��
����FNB=8mg��
�������غ㶨�ɿ�֪����������Ep=mv2B=mgR��
��2����������C����ٶ�ΪvC���������֪��mg=m![]()
������B���˶���C��Ĺ����У��������غ㶨�ɵã�
Q=mvB2����mvC2+2mgR����
��ã�Q=mgR��

��ϰ��ϵ�д�
�����Ŀ