题目内容
一艘宇宙飞船,飞近某一行星,并靠近该星表面的圆形轨道绕行数圈后,着陆在该行星表面上.宇航员在绕行时测出飞船的周期为T,着陆后用弹簧秤测出质量为m的物体重力为F(万有引力常量为G),那么,该星球的质量为( )
A. | B. | C. | D. |
B
解析试题分析:设该行星表面重力加速度为 ,又因宇航员用弹簧秤竖直悬挂质量为m的钩码时,弹簧秤的示数为F,则有:
,又因宇航员用弹簧秤竖直悬挂质量为m的钩码时,弹簧秤的示数为F,则有: ,设行星球半径为
,设行星球半径为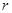 ,在该行星表面有:
,在该行星表面有: 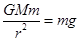 ,飞船在靠近行星表面做匀速圆周运动时,根据万有引力提供向心力,列出等式:
,飞船在靠近行星表面做匀速圆周运动时,根据万有引力提供向心力,列出等式: ,以上三式联立,解得:
,以上三式联立,解得: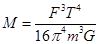 ,故选B。
,故选B。
考点:本题考查了万有引力定律及其应用。

练习册系列答案
相关题目
我国“嫦娥一号”探月卫星发射后,先在“24小时轨道”上绕地球运行(即绕地球一圈需要24小时);然后,经过两次变轨依次到达“48小时轨道”和“72小时轨道”;最后奔向月球.如果按圆形轨道计算,并忽略卫星质量的变化,则在每次变轨完成后与变轨前相比,( )
| A.卫星绕行速度变大 |
| B.卫星所受向心力增大 |
| C.卫星的机械能守恒 |
| D.卫星动能减小,引力势能增大 |
质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的
A.线速度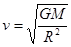 |
B.角速度为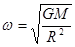 |
C.运行周期为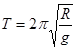 |
D.向心加速度为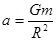 |
设地球表面的重力加速度为g0,物体在距离地面为3R(R是地球半径)空中,由于地球的作用产生的加速度为g,则g/g0为
| A.1/3 | B.1/9 | C.1/4 | D.1/16 |
两个质点之间万有引力的大小为F,如果将这两个质点之间的距离变为原来的2倍,那么它们之间万有引力的大小变为
| A.F/4 | B.4F | C.16F | D.F/16 |
人造地球卫星的第一宇宙速度约为8 km/s,某行星的质量是地球质量的6倍,半径是地球半径的1.5倍.该行星上的第一宇宙速度约为
| A.16 km/s | B.32 km/s | C.46 km/s | D.2 km/s |
关于地球的第一宇宙速度,下列表述正确的是( )
| A.第一宇宙速度又叫脱离速度 |
| B.第一宇宙速度又叫环绕速度 |
| C.第一宇宙速度跟地球的质量无关 |
| D.第一宇宙速度跟地球的半径无关 |
