题目内容
【题目】在xoy平面内，直线OM与x轴负方向成45°角，以OM为边界的匀强电场和匀强磁场如图所示．在坐标原点O有一不计重力的粒子，其质量和电荷量分别为m和＋q，以v0沿x轴正方向运动，粒子每次到x轴将反弹，第一次无能量损失，以后每次反弹水平分速度不变，竖直分速度大小减半、方向相反．电场强度 E=
、磁感应强度B=
．求带电粒子：
⑴第一次经过OM时的坐标；
⑵第二次到达x轴的动能；
⑶在电场中运动时竖直方向上的总路程．
【答案】（1）（-1m、1m）（2）
（3）
m
【解析】（1）粒子进入磁场，根据左手定则，粒子做3/4的圆周运动后经过OM，根据洛伦兹力提供向心力有：qvB＝m
，
代入数据解得：R=1m，
故第一次经过OM时的坐标为（-1m、1m）；
（2）粒子第二次进入磁场，速度不变，则粒子在磁场中运动的半径也为R，故进入电场时离x轴的高度为2R，根据动能定理，粒子到达x轴的动能有：
2qER＝
mv2
mv02，
解得，动能为：Ek＝
mv2＝
；
（3）粒子运轨迹如图所示：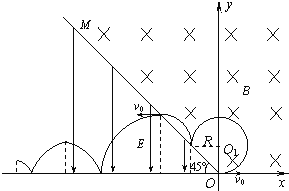
因粒子第二次进入电场做类平抛运动，故到达x轴时的水平分速度为v0，
竖直方向：a＝
vy2＝2ah1
解得：vy＝
，
从类平抛开始，粒子第一次到达最高点离x轴的竖直高度为：h1＝
第二次到达最高点离x轴的竖直高度为：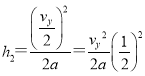 
…
第n次到达最高点离x轴的竖直高度为：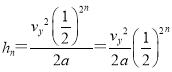 
故从类平抛开始，在竖直方向上往返的总路程为：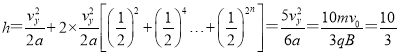 
练习册系列答案
相关题目
