题目内容
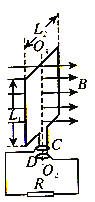
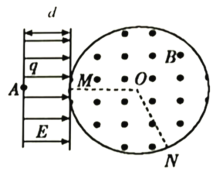
【题目】如图所示,空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场,电场强度为E、场区宽度为d。在紧靠电场右侧的圆形区域内,分布着垂直于纸面向外的匀强磁场。磁感应强度B未知,圆形磁场区域半径为R。一质量为m、电荷量为q的带正电的粒子从A点由静止释放后,在M点离开电场,并沿半径方向射入磁场区域,然后从N点射出,O为圆心,∠MON=120°,粒子重力可忽略不计。求:
(1)粒子经电场加速后,进入磁场时速度的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)若粒子在离开磁场前某时刻,磁感应强度变为垂直纸面向里、大小为B1,此后粒子恰好被束缚在该磁场中,则B1的最小值为多少?
【答案】(1)![]() (2)
(2)![]() (3)(1+
(3)(1+![]() )
)![]()
【解析】
(1)设粒子经电场加速后的速度为v,由动能定理得:
![]() ,
,
解得:
![]() ;
;
(2)粒子运动轨迹如图所示:
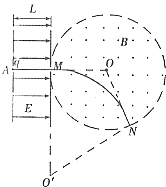
粒子在磁场中做匀速圆周运动,由牛顿第二定律得:
![]() ,
,
由几何知识可得:
tan30=![]() ,
,
解得:
![]() ;
;
(3)粒子运动轨迹如图所示,
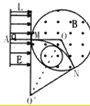
当粒子运动到轨迹与OO′连线交点处改变磁场大小时,粒子的轨道半径最大,磁感应强度最小,
由几何知识可知:
![]() ,
,
由牛顿第二定律得:
![]() ,
,
解得:
![]()

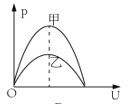
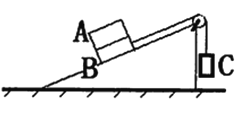
【题目】某同学用图(a)所示的装置测量木块与木板之间的动摩擦因数。跨过光滑定滑轮的细线两端分别与木块和弹簧测力计相连,滑轮和木块间的细线保持水平,在木块上方放置砝码缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧测力计的示数即为木块受到的滑动摩擦力的大小。某次实验所得数据已在下表中给出,其中![]() 的值可从图(b)中弹簧测力计的示数读出。
的值可从图(b)中弹簧测力计的示数读出。
砝码的质量 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 |
滑动摩擦力 | 2.15 | 2.36 | 2.55 |
| 2.93 |
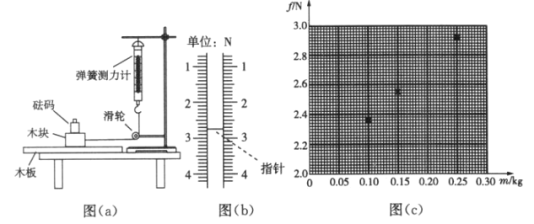
回答下列问题:
(1)![]() =__________
=__________![]() :
:
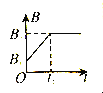
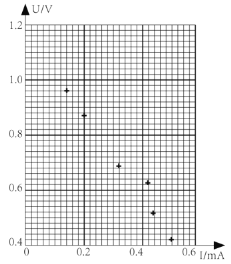
(2)在图(c)的坐标纸上补齐未画出的数据点并绘出![]() 图线____________;
图线____________;
(3)![]() 与
与![]() 、木块质量
、木块质量![]() 、木板与木块之间的动摩擦因数
、木板与木块之间的动摩擦因数![]() 及重力加速度大小
及重力加速度大小![]() 之间的关系式为
之间的关系式为![]() =__________,
=__________,![]() 图线(直线)的斜率的表达式为
图线(直线)的斜率的表达式为![]() =__________。
=__________。
(4)取![]() ,由绘出的
,由绘出的![]() 图线求得
图线求得![]() _____。(保留2位有效数字)
_____。(保留2位有效数字)