题目内容
如图所示，三颗人造地球卫星，b与c半径相同，则（ ）
| A、线速度Vb=Vc＜Va | B、周期Tb=Tc＞Ta | C、b与c的向心加速度大小相等，且大于a的向心加速度 | D、c加速，就可在此时运行的轨道追上b |
分析：人造地球卫星为万有引力充当向心力，故由万有引力公式可得出不同规道上的线速度、角速度及向心加速度的关系．
解答：解：A、根据万有引力等于向心力G
=m
，得线速度v=
，即半径越大，线速度越小，故vb=vc＜va，故A正确；
B、根据万有引力等于向心力G
=m
r，得周期T=2π
，即半径越大，周期越大，故Tb=Tc＞Ta，故B正确；
C、根据万有引力等于向心力G
=ma，得向心力加速度a=
，即半径越大，向心加速度越小，故bc的加速度小于a的加速度，故C错误；
D、c加速，向心力大于万有引力，要做离心运动，轨道半径变大，不可能在原来运行的轨道追上b，故D错误．
故选：AB．
| Mm |
| r2 |
| v2 |
| r |
|
B、根据万有引力等于向心力G
| Mm |
| r2 |
| 4π2 |
| T2 |
|
C、根据万有引力等于向心力G
| Mm |
| r2 |
| GM |
| r2 |
D、c加速，向心力大于万有引力，要做离心运动，轨道半径变大，不可能在原来运行的轨道追上b，故D错误．
故选：AB．
点评：天体的运动中比较各量的变化一定要紧密结合万有引力定律，所有的结论都应是由万有引力推出的．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
如图所示，三颗人造地球卫星的质量Ma=Mb＜Mc，b与c半径相同，则下列说法正确的是（ ）
如图所示，三颗人造地球卫星的质量ma=mb＜mc，b与c半径相同，则下列说法错误的是（ ）
如图所示，三颗人造地球卫星A、B、C绕地球作匀速圆周运动，且卫星的质量mA=mB＞mC，由此可知，则三个卫星（ ）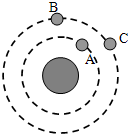
如图所示，三颗人造地球卫星A、B、C绕地球做匀速圆周运动，下列说法正确的是（ ）