题目内容
1.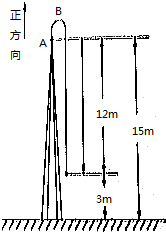 在一高塔上,一人水平伸出手去并以4rn/s的初速度竖直上抛一重物,手离地面高15m(如图),试求(计算时取g=10m/s2):
在一高塔上,一人水平伸出手去并以4rn/s的初速度竖直上抛一重物,手离地面高15m(如图),试求(计算时取g=10m/s2):(1)物体上升的时间;
(2)物体上升的最大高度;
(3)物体下落到原处的时间;
(4)物体下落到原处时的速度;
(5)物体经2s后离地面的高度;
(6)画出全过程的速度图象和位移图象.
分析 (1)竖直上抛运动的上升过程是匀减速直线运动,根据速度时间关系公式列式求解;
(2)最高点的速度等于0,由位移公式即可求出;
(3)竖直上抛运动的整个过程是匀变速直线运动,根据位移时间关系公式列式求解;
(4)根据竖直上抛运动的速度对称性分析;
(5)求解物体运动3s的位移,结合实际情况判断物体3s时刻的位置;
(6)结合速度公式与位移公式即可画出全过程的速度图象和位移图象.
解答 解:(1)竖直上抛运动的上升过程是匀减速直线运动,根据速度时间关系公式,有:
0=v0-gt1
解得:t1=$\frac{{v}_{0}}{g}=\frac{4}{10}=0.4s$
(2)竖直上抛运动是匀变速直线运动,以向上为正方向,初速度为4m/s,加速度为-10m/s2,最高点的速度等于0,所以最大高度:
${h}_{m}=\frac{-{v}_{0}^{2}}{2g}=\frac{-{4}^{2}}{2×(-10)}=0.8$m
(3)物体下落到原处时的位移为0,加速度为-10m/s2,根据位移时间关系公式,有:
x=v0t+$\frac{1}{2}a{t}^{2}$
即:0=4t+$\frac{1}{2}×(-10)×{t}^{2}$
解得:t=0(舍去),t=0.8s
(4)竖直上抛运动上升和下降经过同一位置的速度是相等的,故落回抛出点时的速度:
v1=-v0=-4m/s
负号表示方向向下.
(5)设物体2s内一直运动,以向上为正方向,初速度为4m/s,加速度为-10m/s2,位移为:
x=v0t+$\frac{1}{2}a{t}^{2}$=4×2+$\frac{1}{2}×(-10)×{2}^{2}$=-12m,即物块要在抛出点下方12m位置;
距离地面的高度为:H=h+x=15+(-12)=3m
(6)选取向上为正方向,则物体运动的速度:v=v0-gt=4-10t
物体的位移:$x={v}_{0}t-\frac{1}{2}g{t}^{2}$=4t-5t2
物体落地时的位移为-15m,代入位移公式得:
$t=\frac{4+\sqrt{316}}{10}≈2.18$s
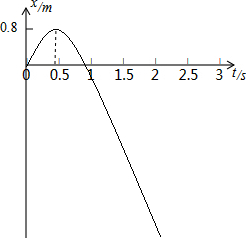
结合速度公式与位移公式即可画出全过程的速度图象和位移图象如图.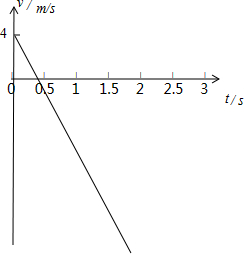
答:(1)物体到达最高点的时间为0.4s;
(2)物体上升的最大高度是0.8m;
(3)物体落回抛出点的时间为0.8s;
(4)物体落回抛出点时的速度方向向下,大小为4m/s;
(5)物体2s后距地面的高度为3m.
(6)如图
点评 本题关键明确竖直上抛运动是匀变速直线运动,上升和下降过程具有对称性,然后结合运动学公式列式求解.

 阅读快车系列答案
阅读快车系列答案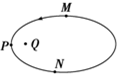 如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下,做以Q为焦点的椭圆运动.M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.电子在从M点经P到达N点的过程中( )
如图所示,带正电的点电荷固定于Q点,电子在库仑力作用下,做以Q为焦点的椭圆运动.M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.电子在从M点经P到达N点的过程中( )| A. | 速率先减小后增大 | B. | 速率先增大后减小 | ||
| C. | 电势能先减小后增大 | D. | 电势能先增大后减小 |
| A. | EA=EB | B. | EA<EB | C. | φA<φB | D. | φA>φB |
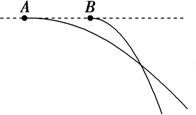 在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须( )
在同一水平直线上的两位置分别沿同方向抛出两小球A和B,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须( )| A. | 先抛出A球 | B. | 先抛出B球 | ||
| C. | 同时抛出两球 | D. | B球的初速度大于A球的初速度 |
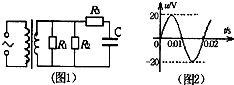
| A. | 原线圈输入电压的有效值为400V | B. | 交流电的频率为50Hz | ||
| C. | 电容器 C 所带电量恒值为2×l0-3C | D. | 电阻R1消耗的电功率为20W |
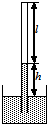 如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体长度为l,管内外水银面高度差为h,若保持玻璃管不动,向水银槽内加入少许水银,则( )
如图,开口向下的玻璃管插入水银槽中,管内封闭了一段气体,气体长度为l,管内外水银面高度差为h,若保持玻璃管不动,向水银槽内加入少许水银,则( )| A. | l增大,h增大 | B. | l减小,h增大 | C. | l增大,h减小 | D. | l减小,h减小 |
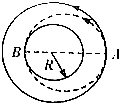 宇宙飞船飞临一颗半径为R的未知行星,在距行星表面也为R的圆轨道上做匀速圆周运动,周期为T(如图),宇宙飞船在A点沿圆周的切线方向发射一个探测器,使之沿椭圆轨道运动,恰好在B点掠过行星表面后又能回到A点.已知引力常量为G.问:
宇宙飞船飞临一颗半径为R的未知行星,在距行星表面也为R的圆轨道上做匀速圆周运动,周期为T(如图),宇宙飞船在A点沿圆周的切线方向发射一个探测器,使之沿椭圆轨道运动,恰好在B点掠过行星表面后又能回到A点.已知引力常量为G.问: