题目内容
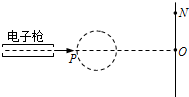
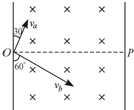
电视机的显象管中,电子束的偏转是用磁偏转技术实现的.在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过圆形区域后,打到荧光屏上,如图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点.已知ON=h,PO=L.电子的电荷量为e,质量为m.求:
(1)电子打到荧光屏上的N点时的动能是多少?说明理由.
(2)电子在磁场中做圆周运动的半径R是多少?
(3)试推导圆形区域的半径r与R及h、L的关系式.(已知tan2θ=
)
(1)电子打到荧光屏上的N点时的动能是多少?说明理由.
(2)电子在磁场中做圆周运动的半径R是多少?
(3)试推导圆形区域的半径r与R及h、L的关系式.(已知tan2θ=
| 2tanθ |
| 1-2tan2θ |

(1)电子经过偏转磁场时洛伦兹力不做功,电子的动能仍为E.
(2)E=
mv2 则v=
由牛顿第二定律,evB=m
得:圆周运动的半径R=
(3)如图所示,电子在偏转磁场中做圆周运动的圆心为O1,圆形区域的圆心为O2.
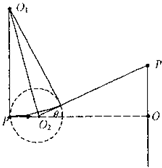
电子从磁场圆射出时的速度方向与O2O的夹角设为θ,
有tanθ=
tan
=
由半角公式可得:
=
=
答:(1)电子打到荧光屏上的N点时的动能是E,洛伦兹力不做功.
(2)电子在磁场中做圆周运动的半径R是
.
(3)圆形区域的半径r与R及h、L的关系式为
=
.
(2)E=
| 1 |
| 2 |
|
由牛顿第二定律,evB=m
| v2 |
| R |
得:圆周运动的半径R=
| ||
| eB |
(3)如图所示,电子在偏转磁场中做圆周运动的圆心为O1,圆形区域的圆心为O2.

电子从磁场圆射出时的速度方向与O2O的夹角设为θ,
有tanθ=
| h |
| L-r |
| θ |
| 2 |
| r |
| R |
由半角公式可得:
| h |
| L-r |
| ||
1-(
|
| 2Rr |
| R2-r2 |
答:(1)电子打到荧光屏上的N点时的动能是E,洛伦兹力不做功.
(2)电子在磁场中做圆周运动的半径R是
| ||
| eB |
(3)圆形区域的半径r与R及h、L的关系式为
| h |
| L-r |
| 2Rr |
| R2-r2 |

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目


 。
。