题目内容
5. 两根长度均为L的绝缘细线分别系住质量相等,电荷量均为+Q的小球a、b,并悬挂在O点.当两个小球静止时,它们处在同一高度上,且两细线与竖直方向的夹角均为α=60°,如图所示,静电力常量为k,则每个小球的质量为( )
两根长度均为L的绝缘细线分别系住质量相等,电荷量均为+Q的小球a、b,并悬挂在O点.当两个小球静止时,它们处在同一高度上,且两细线与竖直方向的夹角均为α=60°,如图所示,静电力常量为k,则每个小球的质量为( )| A. | $\frac{kQ^2}{9gL^2}$ | B. | $\frac{\sqrt{3}kQ^2}{9gL^2}$ | C. | $\frac{kQ^2}{3gL^2}$ | D. | $\frac{\sqrt{3}kQ^2}{3gL^2}$ |
分析 对其中一个小球受力分析,由共点力的平衡条件可得出小球所受重力的大小和小球受到的库仑力大小关系,由库仑力公式可得出小球受到的库仑力的大小,再求得小球的质量.
解答  解:对小球进行受力分析,如图所示.设绳子对小球的拉力为T,
解:对小球进行受力分析,如图所示.设绳子对小球的拉力为T,
根据平衡条件,结合三角知识,可得:$\frac{{F}_{C}}{mg}$=tanα=$\sqrt{3}$,
根据库仑定律得,小球在水平方向受到库仑力的大小为:FC=$\frac{k{Q}^{2}}{{r}^{2}}$,
而由几何关系,则有:r=$\sqrt{3}$L
解得:m=$\frac{\sqrt{3}k{Q}^{2}}{9g{L}^{2}}$,故B正确,ACD错误;
故选:B.
点评 本题两边的球是对称的,故分析其中一个小球即可得出正确结论;
在电场中处理问题的方法与力学是一致的,做好受力分析是解决问题的关键.

练习册系列答案
相关题目
16.关于固体和液体,下列说法正确的是( )
| A. | 由于液体表面分子间距离大于液体内部分子间的距离,液面分子间只有引力,没有斥力,所以液体表面具有收缩的趋势 | |
| B. | 液晶既具有液体的流动性,又具有光学各向异性 | |
| C. | 具有规则几何形状的物体一定是晶体 | |
| D. | 有的物质能够生成多种不同的晶体,因为它们的物质微粒能够形成不同的空间结构 |
13.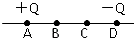 如图,真空中一条直线上有四点A、B、C、D,AB=BC=CD,只在A点放一电量为+Q的点电荷时,B点电场强度为E,若又将等量异号的点电荷-Q放在D点,则( )
如图,真空中一条直线上有四点A、B、C、D,AB=BC=CD,只在A点放一电量为+Q的点电荷时,B点电场强度为E,若又将等量异号的点电荷-Q放在D点,则( )
 如图,真空中一条直线上有四点A、B、C、D,AB=BC=CD,只在A点放一电量为+Q的点电荷时,B点电场强度为E,若又将等量异号的点电荷-Q放在D点,则( )
如图,真空中一条直线上有四点A、B、C、D,AB=BC=CD,只在A点放一电量为+Q的点电荷时,B点电场强度为E,若又将等量异号的点电荷-Q放在D点,则( )| A. | B点电场强度为$\frac{3}{4}$E,方向水平向右 | B. | B点电场强度为$\frac{5}{4}$E,方向水平向左 | ||
| C. | BC线段的中点电场强度为零 | D. | B、C两点的电场强度相同 |
20.在真空中,两点电荷相距0.1m,带电量分别为3×10-7C和-2×10-5C,己知静电力常量k=9×109N•m2/C2,则该两点电荷间的库仑力为( )
| A. | 斥力,5.4N | B. | 引力,5.4N | C. | 斥力,0.54N | D. | 引力,0.54N |
17. 如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )
如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )
 如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )
如图所示为某个电场的部分电场线,把A、B两点的场强记作EA、EB,A、B两点的电势分别记作φA、φB,则( )| A. | φA>φB,EA>EB | B. | φA<φB,EA<EB | C. | φA>φB,EA<EB | D. | φA<φB,EA>EB |
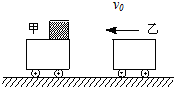 如图所示,甲车质量为m1=2kg,静止在光滑水平面上,上表面光滑,右端放一个质量为m=1kg的小物体.乙车质量为m2=4kg,以v0=5m/s的速度向左运动,与甲车碰撞后,甲车获得v1=8m/s的速度,物体滑到乙车上..若乙车足够长,上表面与物体的动摩擦因数为μ=0.2,求:
如图所示,甲车质量为m1=2kg,静止在光滑水平面上,上表面光滑,右端放一个质量为m=1kg的小物体.乙车质量为m2=4kg,以v0=5m/s的速度向左运动,与甲车碰撞后,甲车获得v1=8m/s的速度,物体滑到乙车上..若乙车足够长,上表面与物体的动摩擦因数为μ=0.2,求: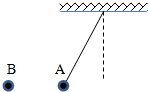 如图所示,把质量为$\frac{\sqrt{3}}{10}$克的带电小球A用丝线吊起,若将带电量为4×10-8C的正电小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为30°,(取g=10m/s2,k=9.0×109N•m2/kg2)求:
如图所示,把质量为$\frac{\sqrt{3}}{10}$克的带电小球A用丝线吊起,若将带电量为4×10-8C的正电小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为30°,(取g=10m/s2,k=9.0×109N•m2/kg2)求: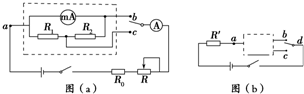
 对改装电表的3mA挡进行校准,校准时需选取的刻度为0.5、1.0、1.5、2.0、2.5、3.0mA.电池的电动势为1.5V,内阻忽略不计;定值电阻R0有两种规格,阻值分别为300Ω和1 000Ω;滑动变阻器R有两种规格,最大阻值分别为750Ω和3000Ω.则R0应选用阻值为300Ω的电阻,R应选用最大阻值为3000Ω的滑动变阻器.
对改装电表的3mA挡进行校准,校准时需选取的刻度为0.5、1.0、1.5、2.0、2.5、3.0mA.电池的电动势为1.5V,内阻忽略不计;定值电阻R0有两种规格,阻值分别为300Ω和1 000Ω;滑动变阻器R有两种规格,最大阻值分别为750Ω和3000Ω.则R0应选用阻值为300Ω的电阻,R应选用最大阻值为3000Ω的滑动变阻器. 如图所示,A、B、C三点在一条直线上,各点都有一个点电荷,它们所带电量相等.A、B两处为正电荷,C处为负电荷,且BC=2AB,那么A、B、C三个点电荷所受库仑力的大小之比为32:45:13.
如图所示,A、B、C三点在一条直线上,各点都有一个点电荷,它们所带电量相等.A、B两处为正电荷,C处为负电荷,且BC=2AB,那么A、B、C三个点电荷所受库仑力的大小之比为32:45:13.