题目内容
13.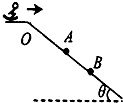 如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )
如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )| A. | tA>tB | B. | tA<tB | C. | θA=θB | D. | θA<θB |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据下降的高度比较运动的时间,抓住速度方向与水平方向夹角是位移与水平方向夹角的正切值的2倍,得出落在斜面上速度与水平方向的夹角.
解答 解:根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}$,因为hA<hB,则tA<tB.
根据tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得,t=$\frac{2{v}_{0}tanθ}{g}$,
设速度方向与水平方向夹角为α,tanα=$\frac{{v}_{y}}{{v}_{0}}=\frac{gt}{{v}_{0}}$,可知tanα=2tanθ,因为位移与水平方向夹角相同,则速度与水平方向的夹角相同,故B、C正确,A、D错误.
故选:BC.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,要注意本题是一个位移限制,即竖直位移和水平位移的比值是一定量.

练习册系列答案
相关题目
3.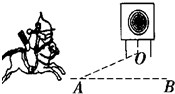 如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )
如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )
 如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )
如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )| A. | 箭射到固定目标的最短时间为$\frac{d}{{v}_{1}}$ | |
| B. | 箭射到固定目标的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ | |
| C. | 运动员放箭处离固定目标的距离为$\frac{{v}_{1}}{{v}_{2}}$d | |
| D. | 运动员放箭处离固定目标的距离为$\frac{\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$d |
4.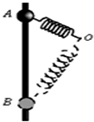 如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,现将小球从A点由静止释放,沿竖直杆下降到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹性势能相等.关于小球从A运动到B的过程,下列说法正确的是( )
如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,现将小球从A点由静止释放,沿竖直杆下降到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹性势能相等.关于小球从A运动到B的过程,下列说法正确的是( )
 如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,现将小球从A点由静止释放,沿竖直杆下降到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹性势能相等.关于小球从A运动到B的过程,下列说法正确的是( )
如图所示,一质量为m的小球套在光滑竖直杆上,轻质弹簧一端固定于O点,另一端与该小球相连,现将小球从A点由静止释放,沿竖直杆下降到B点,已知OA长度小于OB长度,弹簧处于OA、OB两位置时弹性势能相等.关于小球从A运动到B的过程,下列说法正确的是( )| A. | 从A到B的过程中,小球动能的变化量与重力做的功相等 | |
| B. | 弹簧弹力对小球先做正功再做负功 | |
| C. | 加速度等于重力加速度g的位置只有一个 | |
| D. | 弹簧弹力的功率为零的位置有三个 |
8.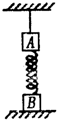 如图所示,A物块质量为2m,B物抉质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触(压力为O),此时轻弹簧的伸长量为x,现将悬绳剪断,下列判断正确的是( )
如图所示,A物块质量为2m,B物抉质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触(压力为O),此时轻弹簧的伸长量为x,现将悬绳剪断,下列判断正确的是( )
 如图所示,A物块质量为2m,B物抉质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触(压力为O),此时轻弹簧的伸长量为x,现将悬绳剪断,下列判断正确的是( )
如图所示,A物块质量为2m,B物抉质量为m,用一轻弹簧相连,将A用长度适当的轻绳悬挂于天花板上,系统处于静止状态,B物块恰好与水平桌面接触(压力为O),此时轻弹簧的伸长量为x,现将悬绳剪断,下列判断正确的是( )| A. | 悬绳剪断瞬间A物块的加速度大小为2g | |
| B. | 悬绳剪断瞬间A物块的加速度大小为$\frac{3}{2}$g | |
| C. | 悬绳剪断后A物块向下运动距离2x时速度最大 | |
| D. | 悬绳剪断后A物块向下运动距离x时加速度最小 |
18.某同学在学习了动力学知识后,绘出了一个沿直线运动的物体的位移x、速度v、加速度a随时间变化的图象如图所示,若该物体在t=0时刻,初速度均为零,则下列图象中表示该物体在t=6s内位移为0的是( )
| A. | 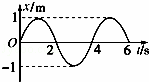 | B. | 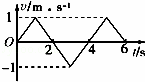 | ||
| C. | 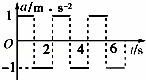 | D. | 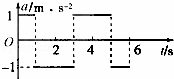 |
5.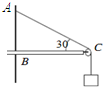 如图所示,水平横杆BC的B端固定,C端有一定滑轮,跨在定滑轮上的绳子一端悬挂质量为10kg的物体,另一端固定在A点,当物体静止时,∠ACB=30°,则此时定滑轮对绳子的作用力为(不计定滑轮和绳子的质量,忽略一切摩擦,g=10m/s2)( )
如图所示,水平横杆BC的B端固定,C端有一定滑轮,跨在定滑轮上的绳子一端悬挂质量为10kg的物体,另一端固定在A点,当物体静止时,∠ACB=30°,则此时定滑轮对绳子的作用力为(不计定滑轮和绳子的质量,忽略一切摩擦,g=10m/s2)( )
 如图所示,水平横杆BC的B端固定,C端有一定滑轮,跨在定滑轮上的绳子一端悬挂质量为10kg的物体,另一端固定在A点,当物体静止时,∠ACB=30°,则此时定滑轮对绳子的作用力为(不计定滑轮和绳子的质量,忽略一切摩擦,g=10m/s2)( )
如图所示,水平横杆BC的B端固定,C端有一定滑轮,跨在定滑轮上的绳子一端悬挂质量为10kg的物体,另一端固定在A点,当物体静止时,∠ACB=30°,则此时定滑轮对绳子的作用力为(不计定滑轮和绳子的质量,忽略一切摩擦,g=10m/s2)( )| A. | N=100$\sqrt{3}$ N,水平向右 | B. | N=200N,与水平成30°斜向上 | ||
| C. | N=100$\sqrt{3}$N,与水平成30°斜向上 | D. | N=100N,与水平成30°斜向上 |
2.一个滑块以初速度v0从够长的固定斜面底端沿斜面向上运动,经2t0时间返回到斜面底端.如图所示图象表示该滑块在此斜面上运动过程中速度的大小v随时间t变化的规律,其中可能正确的是( )
| A. | 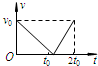 | B. |  | C. |  | D. | 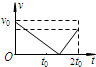 |
3.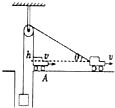 如图所示,某小车将一质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高为h,开始时物体静止于A点,且滑轮两侧的绳都竖直绷紧,汽车以速度v水平向右匀速直线运动,至汽车与连接的细绳水平方向的夹角为60°,(不计一切摩擦)则( )
如图所示,某小车将一质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高为h,开始时物体静止于A点,且滑轮两侧的绳都竖直绷紧,汽车以速度v水平向右匀速直线运动,至汽车与连接的细绳水平方向的夹角为60°,(不计一切摩擦)则( )
 如图所示,某小车将一质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高为h,开始时物体静止于A点,且滑轮两侧的绳都竖直绷紧,汽车以速度v水平向右匀速直线运动,至汽车与连接的细绳水平方向的夹角为60°,(不计一切摩擦)则( )
如图所示,某小车将一质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高为h,开始时物体静止于A点,且滑轮两侧的绳都竖直绷紧,汽车以速度v水平向右匀速直线运动,至汽车与连接的细绳水平方向的夹角为60°,(不计一切摩擦)则( )| A. | 在运动过程中,物体m一直做加速运动 | |
| B. | 运动过程中,细绳对物体的拉力总是等于mg | |
| C. | 在绳与水平方向的夹角为60°时,物体m上升的速度为$\frac{v}{2}$ | |
| D. | 在绳与水平方向的夹角为60°时,拉力功率等于$\frac{1}{2}$mgv |
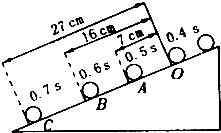 让小球从斜面的顶端滚下(如图所示).0.4s、0.5s、0.6s、0.7s时刻,小球分别位于O、A、B、C点,各点到O点的距离已标在图中,试计算:
让小球从斜面的顶端滚下(如图所示).0.4s、0.5s、0.6s、0.7s时刻,小球分别位于O、A、B、C点,各点到O点的距离已标在图中,试计算: