题目内容
3. 如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )
如图所示,民族运动会上有一个骑射项目,运动员骑在奔驰的马背上沿跑道AB运动,拉弓放箭射向他左侧的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭速度为v2,跑道离固定目标的最近距离OA=d.若不计空气阻力的影响,要想命中固定目标且射出的箭在空中飞行时间最短,则( )| A. | 箭射到固定目标的最短时间为$\frac{d}{{v}_{1}}$ | |
| B. | 箭射到固定目标的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ | |
| C. | 运动员放箭处离固定目标的距离为$\frac{{v}_{1}}{{v}_{2}}$d | |
| D. | 运动员放箭处离固定目标的距离为$\frac{\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$d |
分析 运动员放出的箭既参与了沿马运行方向上的匀速直线运动,又参与了垂直于马运行方向上的匀速直线运动,当放出的箭垂直于马运行方向发射,此时运行时间最短,根据t=$\frac{d}{{v}_{2}}$ 求出最短时间,根据分运动和合运动具有等时性,求出箭在马运行方向上的距离,根据运动的合成,求出运动员放箭处离目标的距离.
解答 解:A、当放出的箭垂直于马运行方向发射,此时运行时间最短,所以最短时间t=$\frac{d}{{v}_{2}}$,故AB错误;
C、当放出的箭垂直于马运行方向发射,此时运行时间最短,所以最短时间t=$\frac{d}{{v}_{2}}$,
则箭在沿马运行方向上的位移为x=v1t=$\frac{{v}_{1}}{{v}_{2}}$d
所以放箭处距离目标的距离为s=$\sqrt{{d}^{2}+(\frac{{v}_{1}}{{v}_{2}}d)^{2}}$=$\frac{\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{{v}_{2}}$d,故C错误、D正确.
故选:D.
点评 解决本题的关键知道箭参与了沿马运行方向上的匀速直线运动和垂直于马运行方向上的匀速直线运动,知道分运动与合运动具有等时性.

练习册系列答案
相关题目
14.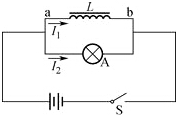 如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
 如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )
如图所示电路为演示自感电路的实验电路,实验时,先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡A的电流为I2,小灯泡处于正常发光状态.迅速断开开关S,可以观察到小灯泡闪亮一下后熄灭,在灯泡闪亮的短暂过程中,以下说法正确的是( )| A. | 线圈L中的电流I1立即减为零 | |
| B. | 线圈L的b端电势高于a端 | |
| C. | 小灯泡A中的电流由I1逐渐减为零,方向与I2相反 | |
| D. | 小灯泡A中的电流I2逐渐减为零,方向与原来相反 |
18. 早在19世纪,匈牙利物理学家厄缶就指出:“沿水平地面向东运动的物体,对地面的压力一定要减轻.”人们把这类现象称为“厄缶效应”.如图所示:我们设想,已知地球的半径R及地球的自转周期T,在地球赤道上,有一列质量是M的列车,当它静止时,考虑地球自转的影响(即火车正随地球自转做线速度为$\frac{2πR}{T}$的圆周运动)时,火车对轨道的压力为N;当火车正以速率v沿水平轨道匀速向东行驶时(即火车相对地面又附加了一个线速度v),设此时火车对轨道的压力为N′,那么因火车向东行驶而引起火车对轨道压力减轻的数值(N-N′)为( )
早在19世纪,匈牙利物理学家厄缶就指出:“沿水平地面向东运动的物体,对地面的压力一定要减轻.”人们把这类现象称为“厄缶效应”.如图所示:我们设想,已知地球的半径R及地球的自转周期T,在地球赤道上,有一列质量是M的列车,当它静止时,考虑地球自转的影响(即火车正随地球自转做线速度为$\frac{2πR}{T}$的圆周运动)时,火车对轨道的压力为N;当火车正以速率v沿水平轨道匀速向东行驶时(即火车相对地面又附加了一个线速度v),设此时火车对轨道的压力为N′,那么因火车向东行驶而引起火车对轨道压力减轻的数值(N-N′)为( )
 早在19世纪,匈牙利物理学家厄缶就指出:“沿水平地面向东运动的物体,对地面的压力一定要减轻.”人们把这类现象称为“厄缶效应”.如图所示:我们设想,已知地球的半径R及地球的自转周期T,在地球赤道上,有一列质量是M的列车,当它静止时,考虑地球自转的影响(即火车正随地球自转做线速度为$\frac{2πR}{T}$的圆周运动)时,火车对轨道的压力为N;当火车正以速率v沿水平轨道匀速向东行驶时(即火车相对地面又附加了一个线速度v),设此时火车对轨道的压力为N′,那么因火车向东行驶而引起火车对轨道压力减轻的数值(N-N′)为( )
早在19世纪,匈牙利物理学家厄缶就指出:“沿水平地面向东运动的物体,对地面的压力一定要减轻.”人们把这类现象称为“厄缶效应”.如图所示:我们设想,已知地球的半径R及地球的自转周期T,在地球赤道上,有一列质量是M的列车,当它静止时,考虑地球自转的影响(即火车正随地球自转做线速度为$\frac{2πR}{T}$的圆周运动)时,火车对轨道的压力为N;当火车正以速率v沿水平轨道匀速向东行驶时(即火车相对地面又附加了一个线速度v),设此时火车对轨道的压力为N′,那么因火车向东行驶而引起火车对轨道压力减轻的数值(N-N′)为( )| A. | $\frac{M{v}^{2}}{R}$ | B. | M[$\frac{{v}^{2}}{R}$+2($\frac{2π}{T}$)v] | C. | M($\frac{2π}{T}$)v | D. | M[$\frac{{v}^{2}}{R}$+($\frac{2π}{T}$)v] |
8. 一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
 一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )| A. | 动能一定增加 | B. | 电势能一定增加 | ||
| C. | 动能和电势能之和一定增加 | D. | 动能和电势能之和一定不变 |
15.在2008年北京奥运会中,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
| A. | 200m决赛中的路程是100m决赛中的路程两倍 | |
| B. | 200m决赛中的位移大小是100m决赛中的位移大小两倍 | |
| C. | 100m决赛中的平均速度约为10.32m/s | |
| D. | 200m决赛中的平均速度约为10.36m/s |
12.关于竖直上抛运动,下列说法中正确的是( )
| A. | 在最高点速度为零,加速度也为零 | |
| B. | 上升过程中速度向上,加速度向下 | |
| C. | 在最高点速度为零,物体处于平衡状态 | |
| D. | 上升到某一高度时的速度与下降到此高度时的速度大小相等 |
13. 如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )
如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )
 如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )
如图所示,两滑雪运动员从0点分别以速度VA和VB水平滑出,分别落到斜坡上的A、B两点,在落点前瞬间速度与水平方向夹角分别为θA与θB,两者在空中运动的时间分别为tA与tB,则( )| A. | tA>tB | B. | tA<tB | C. | θA=θB | D. | θA<θB |
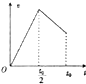
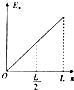
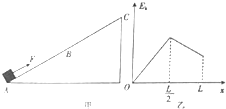 如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )
如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )

 某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验,实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在如图A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.
某实验小组利用拉力传感器、光电门等器材探究滑块“动能定理”的实验,实验装置如图所示,在滑块上安装一遮光条与拉力传感器,把滑块放在水平气垫导轨上并静止在A处,并通过定滑轮的细绳与钩码相连,光电门安装在B处.测得滑块(含遮光板和拉力传感器)质量为M、钩码总质量为m、AB之间的距离为L,当地的重力加速度为g.将滑块在如图A位置由静止释放后,拉力传感器记录下滑块在运动过程的拉力为F,光电计时器记录下遮光条通过光电门的时间分别为△t.