题目内容
【题目】在动摩擦因数μ＝0.2的粗糙绝缘足够长的水平滑漕中，长为2L的绝缘轻质细杆两端各连接一个质量均为m的带电小球A和B，如图为俯视图（槽两侧光滑）。A球的电荷量为＋2q，B球的电荷量为－3q（均可视为质点，也不考虑两者间相互作用的库仑力）。现让A处于如图所示的有界匀强电场区域MPQN内，已知虚线MP恰位于细杆的中垂线，MP和NQ的距离为3L，匀强电场的场强大小为E＝1.2mg/q，方向水平向右。释放带电系统，让A、B从静止开始运动（忽略小球运动中所产生的磁场造成的影响）。求：
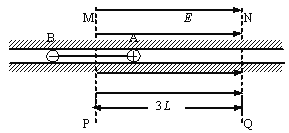
（1）小球B第一次到达电场边界MP所用的时间；
（2）小球A第一次离开电场边界NQ时的速度大小
（3）带电系统运动过程中，B球电势能增加量的最大值。
【答案】（1）
（2）
（3）3.96mgL
【解析】
（1）带电系统开始运动后，先向右加速运动；当B进入电场区时，开始做减速运动．设B进入电场前的过程中，系统的加速度为
，由牛顿第二定律：
，即：
，B刚进入电场时，由：
，可得：
。
（2）当A刚滑到右边界时，电场力对系统做功为：
，摩擦力对系统做功为：
，
，故A球从右端滑出。设B从静止到刚进入电场的速度为
，
，设B进入电场后，系统的加速度为
，由牛顿第二定律：
，
，系统做匀减速运动，设小球A第一次离开电场边界NQ时的速度大小为
；由：
，可得：
。
（3）当带电系统速度第一次为零，此时A已经到达右边界NQ外，B克服电场力做的功最多，B增加的电势能最多，设此时A离右边界NQ的距离为
，由动能定理：
，可得：
，所以B电势能增加的最大值
。
练习册系列答案
53随堂测系列答案
相关题目
