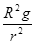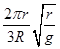题目内容
假设国际编号为“3463”的小行星“高锟星”为均匀的球体,其质量为地球质量的1/k,半径为地球半径的1/q,则其表面的重力加速度是地球表面重力加速度的( )
A.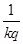 | B.kq | C.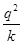 | D.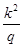 |
C
解析试题分析:根据物体在行星表面所受重力约等于行星对它的万有引力,有:mg=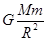 ,解得:g=
,解得:g=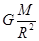 ,所以“高锟星”表面的重力加速度与地球表面重力加速度的比为:
,所以“高锟星”表面的重力加速度与地球表面重力加速度的比为: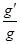 =
=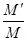 ·
·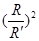 =
=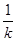 ·q2,故选项C正确。
·q2,故选项C正确。
考点:本题主要考查了万有引力定律的应用问题,属于中档题。

质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的 ( )
A.线速度v=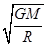 | B.角速度ω= |
C.运行周期T=2π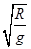 | D.向心加速度a=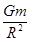 |
美国科学家通过射电望远镜观察到宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统:三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行。设每个星体的质量均为M,忽略其它星体对它们的引力作用,则
A.环绕星运动的角速度为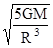 |
B.环绕星运动的线速度为 |
C.环绕星运动的周期为4π |
D.环绕星运动的周期为2π |
未发射的卫星放在地球赤道上随地球自转时的线速度为v1、加速度为a1;发射升空后在近地轨道上做匀速圆周运动时的线速度为v2、加速度为a2;实施变轨后,使其在同步卫星轨道上做匀速圆周运动,运动的线速度为v3、加速度为a3.则v1、v2、v3和a1、a2、a3的大小关系是( )
| A.v2>v3>v1 a2>a3>a1 |
| B.v3>v2>v1 a2>a3>a1 |
| C.v2>v3=v1 a2=a1>a3 |
| D.v2>v3>v1 a3>a2>a1 |
一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,速度大小减小为原来的 ,则变轨前后卫星的
,则变轨前后卫星的
| A.向心加速度大小之比为4:1 | B.角速度大小之比为2:1 |
| C.周期之比为1:8 | D.轨道半径之比为1:2 |
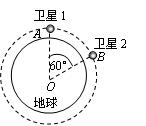
2012年9月采用一箭双星的方式发射了“北斗导航卫星系统”(BDS)系统中的两颗圆轨道半径均为21332km的“北斗-M5”和“北斗M-6”卫星,其轨道如图所示。关于这两颗卫星,下列说法正确的是( )
| A.两颗卫星绕地球运行的向心加速度大小相等 |
| B.两颗卫星绕地球的运行速率均大于7.9km/s |
| C.北斗-M5绕地球的运行周期大于地球的自转周期 |
| D.北斗-M6绕地球的运行速率大于北斗-M5的运行速率 |
如图所示,在火星与木星轨道之间有一小行星带.假设该带中的小行星只受到太阳的引力,并绕太阳做匀速圆周运动.下列说法正确的是( )
| A.太阳对各小行星的引力相同 |
| B.各小行星绕太阳运动的周期均小于一年 |
| C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值 |
| D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值 |