题目内容
如图所示，在火星与木星轨道之间有一小行星带．假设该带中的小行星只受到太阳的引力，并绕太阳做匀速圆周运动．下列说法正确的是（ ）
| A．太阳对各小行星的引力相同 |
| B．各小行星绕太阳运动的周期均小于一年 |
| C．小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值 |
| D．小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值 |
C
解析试题分析:由于各小行星的质量不同，所以太阳对各小行星的引力可能不同，故A错误.根据万有引力提供向心力得：
,得：
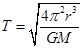，则离太阳越远，周期越大，所以各小行星绕太阳运动的周期大于地球的公转周期，故B错误．根据万有引力提供向心力得：
，则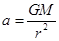
，所以小行星带内侧小行星的向心加速度大于外侧小行星的向心加速度值，故C正确.根据万有引力提供向心力得：
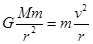,有：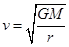
，所以小行星带内各小行星圆周运动的线速度值小于地球公转的线速度值，故D错误.故选C．
考点：本题考查了万有引力定律及其应用.
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案已知万有引力常量为G，地球半径为R，地球表面重力加速度g和地球自转周期T，不考虑地球自转的影响，利用以下条件可求出的物理量是
| A．地球的质量 | B．地球与其同步卫星之间的引力 |
| C．第一宇宙速度 | D．地球同步卫星的高度 |
探月热方兴未艾，我国研制的月球卫星“嫦娥一号”、“嫦娥二号”均已发射升空，“嫦娥三号”预计在2013年发射升空。假设“嫦娥三号”在地球表面的重力为G1，在月球表面的重力为G2；地球与月球均视为球体，其半径分别为R1、R2；地球表面重力加速度为g。则
A．月球表面的重力加速度为 |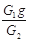
B．月球与地球的质量之比为 |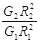
C．月球卫星与地球卫星分别绕月球表面附近与地球表面附近运行的速度之比为 |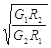
D．“嫦娥三号”环绕月球表面附近做匀速圆周运动的周期为 |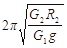
2011年8月26日消息，英国曼彻斯特大学的天文学家认为，他们已经在银河系里发现一颗由曾经的庞大恒星转变而成的体积较小的行星，这颗行星完全由钻石构成。若已知万有引力常量，还需知道哪些信息可以计算该行星的质量 （ ）
| A．该行星表面的重力加速度及绕行星运行的卫星的轨道半径 |
| B．该行星的自转周期与星体的半径 |
| C．围绕该行星做圆周运动的卫星的公转周期及运行半径 |
| D．围绕该行星做圆周运动的卫星的公转周期及公转线速度 |
一宇宙飞船绕地心做半径为r的匀速圆周运动，飞船舱内有一质量为m的人站在可称体重的台秤上．用R表示地球的半径，g表示地球表面处的重力加速度大小，g′表示宇宙飞船所在处的地球引力加速度大小， a表示宇宙飞船做圆周运动的向心加速度大小，V表示宇宙飞船做圆周运动的线速度大小，FN表示人对秤的压力，下面说法中正确的是（ ）
| A．FN＝0 | B．g′＝ａ | C． | D． |
美国宇航局在2011年12月5日宣布，他们在太阳系外发现了一颗类似地球的、可适合人类居住的行星——“开普勒-22b”，该行星环绕一颗恒星运动的周期为290天，它距离地球约600光年，体积是地球的2.4倍．已知万有引力常量和地球表面的重力加速度，假定该行星环绕这颗恒星运动的轨迹为圆轨道，根据以上信息，下列推理中正确的是( )
| A．若已知该行星的轨道半径，可求出该行星所受的万有引力 |
| B．根据地球的公转周期与轨道半径，可求出该行星的轨道半径 |
| C．若该行星的密度与地球的密度相等，可求出该行星表面的重力加速度 |
| D．若已知该行星的轨道半径，可求出恒星的质量 |
据《科技日报》报道，2020年前我国将发射8颗海洋系列卫星，包括4颗海洋水色卫星、2颗海洋动力环境卫星和2颗海陆雷达卫星，以加强对黄岩岛、钓鱼岛及西沙群岛全部岛屿附近海域的监测。设海陆雷达卫星绕地球做匀速圆周运动的轨道半径是海洋动力环境卫星的n倍，则在相同的时间内（ ）
| A．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的n倍 |
| B．海陆雷达卫星和海洋动力环境卫星到地球球心的连线扫过的面积相等 |
C．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的 倍 |
D．海陆雷达卫星到地球球心的连线扫过的面积是海洋动力环境卫星的 倍 |
质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动。已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的（ ）
A．线速度  | B．角速度ω= |
C．运行周期 | D．向心加速度 |