题目内容

如图所示，质量分别为mA、mB的A、B两物块用轻绳连接放在倾角为θ的斜面上，用始终平行于斜面向上的拉力F拉A，使它们沿斜面匀加速上升，A、B与斜面的动摩擦因数均为μ，为了增加轻绳上的张力，可行的办法是（　　）
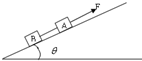
A．增大A物块的质量B．增大B物块的质量
C．增大倾角θD．增大动摩擦因数μ

根据牛顿第二定律得
对整体：F-（mA+mB）gsinθ-μ（mA+mB）gcosθ=（mA+mB）a
得a=
F
mA+mB
-gsinθ-μgcosθ
对B：T-mBgsinθ-μmBgcosθ=mBa
得到，轻线上的张力T=mBgsinθ+μmBgcosθ+mBa=
mBF
mA+mB

则要增加T，可减小A物的质量，或增大B物的质量．
故选：B
练习册系列答案
相关题目
如图所示，光滑斜面CA、DA、EA，三个斜面的倾角分别为60°、45°、30°．物体分别沿三个斜面由顶端从静止滑到底端，下面说法中正确的是（　　）
A．物体沿DA滑到底端时具有最大速率
B．物体沿EA滑到底端所需时间最短
C．物体沿CA下滑，加速度最大
D．物体沿DA滑到底端所需时间最短
一个质量为2kg的物体在两个共点力作用下保持平衡．这两个力的大小分别为25N和20N，则物体此时的加速度大小可能是（　　）
A．1m/s2B．10m/s2C．20m/s2D．30m/s2
传送带是一种常用的运输工具，它被广泛地应用于矿山、码头、货场等生产实际中，在车站、机场等交通场所它也发挥着巨大的作用．如图所示为车站使用的水平传送带装置模型，绷紧的传送带水平部分AB的长度L=5m，并以V传=2m/s的速度向右运动．现将一个可视为质点的旅行包轻轻地无初速地放在传送带的A端，已知旅行包与皮带之间的动摩擦因数μ=0.2．求：
（1）旅行包在传送带上从A端运动到B端所用的时间；
（2）若要旅行包在传送带上从A端运动到B端所用的时间最短，则传动速度的大小应满足什么条件？（g=10m/s2）
如图所示，质量为m1和m2的两物块放在光滑的水平地面上．用轻质弹簧将两物块连接在一起．当用水平力F作用在m1上时，两物块均以加速度a做匀加速运动，此时，弹簧伸长量为x，若用水平力F’作用在m1上时，两物块均以加速度a’=2a做匀加速运动．此时弹簧伸长量为x’．则下列关系正确的是（　　）
A．F’=2FB．x’=2xC．F’＞2FD．x’＜2x
一物体受一对平衡力作用而静止．若其中向东的力先逐渐减小至0，后又逐渐恢复到原来的数值．则该物体（　　）
A．速度方向向东，速度大小不断增大，增至最大时方向仍不变
B．速度方向向西，速度大小不断增大，增至最大时方向仍不变
C．速度方向向东，速度大小先逐渐增大，后逐渐减小到0
D．速度方向向西，速度大小先不断增大，后逐渐减小到0
如图所示为汽车出厂前进行测试的一种情况，其加速过程中牵引力为阻力的3倍，紧急刹车过程完全撤除牵引力．以vJ代替已知的行驶速度（可直接从速度显示表盘上观察记录）、t0代替运行时间（可直接测量），汽车质量为m，设在加速、刹车过程受到的不同阻力保持不变，求：
（1）测试的全程中汽车最大加速度；
（2）加速过程中的阻力；
（3）刹车过程中受到的阻力是加速过程受到的阻力的多少倍？
在验证牛顿运动定律的实验中有如图（a）所示的装置，小车放在斜面上，车前端拴有不可伸长的细线，跨过固定在斜面边缘的小滑轮与重物相连，小车后面与穿过打点计时器的纸带相连．开始时，小车停在靠近打点计时器的位置，重物到地面的距离小于小车到滑轮的距离．启动计时器，释放重物，小车在重物牵引下，由静止开始沿斜面向上运动，重物落地后，小车会继续向上运动一段距离．打点计时器使用的交流电频率为50Hz．图（b）中a、b、c是小车运动纸带上的三段，纸带运动方向如图箭头所示．

（1）根据所+提供的纸带和数据，计算打c段纸带时小车的加速度大小为______m/s2（计算结果保留两位有效数字）．
（2）打a段纸带时，小车的加速度大小是2.5m/s2，请根据加速度的情况，判断小车运动的最大速度可能出现在b段纸带中的______两点之间．
（3）若g取10m/s2，由纸带数据可推算出重物m与小车的质量M之比为m：M=______．
如图所示，一轻质弹簧一端系在墙上的O点，另一端栓住一小物块，弹簧自由伸长时刚好到达B点．今用小物块把弹簧压缩到A点，然后释放，小物块运动到C点时速度为零．物块与水平地面间的动摩擦因数恒定．下列说法正确的是（　　）
A．物块从A到B速度越来越大，从B到C速度越来越小
B．物块从A到B速度越来越大，从B到C加速度增大
C．物块从A到B先加速后减速，从B到C一直做减速运动
D．物块从A到B加速度先减小后增大，从B到C加速度一直增大

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网