题目内容
7. 如图所示,一质量为m的小车静止在光滑的水平面上,在它的横梁上用长为1m的细线悬挂着质量也为m的小球,开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.试求:(取g=10m/s2)
如图所示,一质量为m的小车静止在光滑的水平面上,在它的横梁上用长为1m的细线悬挂着质量也为m的小球,开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.试求:(取g=10m/s2)(1)小球运动到最高点时的速度.
(2)小球上升的最大高度.
(3)小球第一次回到最低点时的速度大小.
分析 开始时给小球一个水平冲量,使小球获得4m/s的水平速度向右运动.小球运动过程中,系统水平方向不受外力,动量守恒,结合能量守恒求出最高点时的速度.
根据系统机械能守恒求解小球上升的最大高度.
解答 解:(1)小球到达最高点与小车具有共同水平速度v′,系统水平动量守恒,
选向右的方向为正,有:
mv=(m+m)v′
代入数据得:v′=2m/s.
(2)根据系统机械能守恒得
$\frac{1}{2}$mv2=$\frac{1}{2}$(m+m)v′2+mgh
h=0.4m,
(3)根据系统水平动量守恒,选向右的方向为正,有:
mv=mv1′+mv″
根据系统机械能守恒得
$\frac{1}{2}$m${v}_{0}^{2}$=$\frac{1}{2}$mv1′2+$\frac{1}{2}$mv″2
解得:mv1′=0,v″=4m/s,或mv1′=4m/s,v″=0,(舍去)
答:(1)小球运动到最高点时的速度是2m/s.
(2)小球上升的最大高度是0.4m.
(3)小球第一次回到最低点时的速度大小是0.
点评 本题是系统水平方向动量守恒和机械能守恒的类型,关键是要抓住临界条件,以及在运用动量守恒定律解题时注意速度的方向.

练习册系列答案
相关题目
17. 如图所示,闭合的矩形导体线圈ABCD在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,沿着OO′方向观察,线圈沿顺时针方向转动.已知匀强磁场的磁感应强度为B,线圈匝数为n,AB边的边长为L1,AD边的边长为L2,线圈电阻为R,转动的角速度为ω,则当线圈转至图示位置时( )
如图所示,闭合的矩形导体线圈ABCD在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,沿着OO′方向观察,线圈沿顺时针方向转动.已知匀强磁场的磁感应强度为B,线圈匝数为n,AB边的边长为L1,AD边的边长为L2,线圈电阻为R,转动的角速度为ω,则当线圈转至图示位置时( )
 如图所示,闭合的矩形导体线圈ABCD在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,沿着OO′方向观察,线圈沿顺时针方向转动.已知匀强磁场的磁感应强度为B,线圈匝数为n,AB边的边长为L1,AD边的边长为L2,线圈电阻为R,转动的角速度为ω,则当线圈转至图示位置时( )
如图所示,闭合的矩形导体线圈ABCD在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动,沿着OO′方向观察,线圈沿顺时针方向转动.已知匀强磁场的磁感应强度为B,线圈匝数为n,AB边的边长为L1,AD边的边长为L2,线圈电阻为R,转动的角速度为ω,则当线圈转至图示位置时( )| A. | 线圈中感应电流的方向为ABCDA | |
| B. | 线圈中的感应电动势为2nBL2ω | |
| C. | 穿过线圈的磁通量的变化率最大 | |
| D. | 线圈AD边所受安培力的大小为$\frac{{n}^{2}{B}^{2}{L}_{1}{L}_{2}ω}{R}$,方向垂直纸面向里 |
15.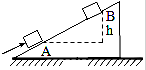 如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
 如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )
如图所示,质量为m的物体,在沿斜面方向的恒力F的作用下,沿粗糙的斜面匀速地由A点运动到B点,物体上升的高度为h,则在运动过程中( )| A. | 物体所受重力做的功为mgh | |
| B. | 恒力F与摩擦力的合力做功为mgh | |
| C. | 物体所受的支持力与摩擦力的合力做功为mgh | |
| D. | 物体所受各力的合力做功为mgh |
12. 如图所示,在波的传播方向上有相距1m的6个质点a、b、c、d、e、f均静止在各自的平衡位置,一列横波以1m/s的水平速度向右传播.此波在t=0时刻到达a质点,a质点开始由平衡位置向下振动,t=1s时质点a第一次到达最低点,则在8s<t<9s这段时间内,下列说法正确的是( )
如图所示,在波的传播方向上有相距1m的6个质点a、b、c、d、e、f均静止在各自的平衡位置,一列横波以1m/s的水平速度向右传播.此波在t=0时刻到达a质点,a质点开始由平衡位置向下振动,t=1s时质点a第一次到达最低点,则在8s<t<9s这段时间内,下列说法正确的是( )
 如图所示,在波的传播方向上有相距1m的6个质点a、b、c、d、e、f均静止在各自的平衡位置,一列横波以1m/s的水平速度向右传播.此波在t=0时刻到达a质点,a质点开始由平衡位置向下振动,t=1s时质点a第一次到达最低点,则在8s<t<9s这段时间内,下列说法正确的是( )
如图所示,在波的传播方向上有相距1m的6个质点a、b、c、d、e、f均静止在各自的平衡位置,一列横波以1m/s的水平速度向右传播.此波在t=0时刻到达a质点,a质点开始由平衡位置向下振动,t=1s时质点a第一次到达最低点,则在8s<t<9s这段时间内,下列说法正确的是( )| A. | 质点c的加速度逐渐增大 | B. | 质点d向下运动 | ||
| C. | 质点b的速度逐渐减小 | D. | 质点f的振幅逐渐变小 |
19.一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是( )
| A. | 增大入射光的频率,金属的逸出功将增大 | |
| B. | 增大入射光的频率,光电子的最大初动能将增大 | |
| C. | 增大入射光的强度,光电子的最大初动能将增大 | |
| D. | 延长入射光照射时间,光电子的最大初动能将增大 |
16. 如图,粗糙绝缘水平面上O、A、B、C四点共线,在O点固定一带正电小球Q,在A点由静止释放带正电小金属块P(可视为质点),P沿OC连线运动,到B点时速度最大,最后停止在C点.则( )
如图,粗糙绝缘水平面上O、A、B、C四点共线,在O点固定一带正电小球Q,在A点由静止释放带正电小金属块P(可视为质点),P沿OC连线运动,到B点时速度最大,最后停止在C点.则( )
 如图,粗糙绝缘水平面上O、A、B、C四点共线,在O点固定一带正电小球Q,在A点由静止释放带正电小金属块P(可视为质点),P沿OC连线运动,到B点时速度最大,最后停止在C点.则( )
如图,粗糙绝缘水平面上O、A、B、C四点共线,在O点固定一带正电小球Q,在A点由静止释放带正电小金属块P(可视为质点),P沿OC连线运动,到B点时速度最大,最后停止在C点.则( )| A. | A点电势低于B点电势 | |
| B. | P在由A向C运动的过程中,电势能一直增大 | |
| C. | 在B点P所受的滑动摩擦力等于库仑力 | |
| D. | 从B到C的过程中,P的动能全部转化为电势能 |
17. 如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )
如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )
 如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )
如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )| A. | 小物体与甲传送带间的动摩擦因数较小 | |
| B. | 两传送带对小物体做功相等 | |
| C. | 两传送带消耗的电能相等 | |
| D. | 两种情况下因摩擦产生的热量相等 |
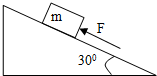 如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2)
如图所示,倾角为30°的斜面上放一质量为10㎏的木块,木块与斜面之间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,用一平行于斜面的力F向上推木块,欲使木块静止在斜面上,求推力F的范围?(假设最大静摩擦力等于滑动摩擦力,g=10m/s2) 如图所示,一块物块m静止在斜面上,斜面匀速地竖直向上移动距离h,则摩擦力、弹力、重力对物块做的功分别为多少?
如图所示,一块物块m静止在斜面上,斜面匀速地竖直向上移动距离h,则摩擦力、弹力、重力对物块做的功分别为多少?