��Ŀ����
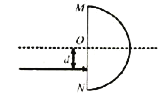
����Ŀ����ͼ��ʾ������ΪM=4kg��ľ�徲ֹ�ڹ⻬ˮƽ���ϣ�һ������Ϊm=1kg��С�����Գ��ٶ�v0=5m/s��ľ���������һ���ľ�壬С����ʼ��δ�뿪ľ�塣������˵����ȷ��

A.�ӿ�ʼ��С������ľ����Ծ�ֹ���ʱ����,С�����ľ��ļ��ٶȴ�С֮��Ϊ1:4
B..������������Ħ������������Ϊ10J
C.�������ľ�����С������3.5m
D.�ӿ�ʼ��С������ľ����Ծ�ֹ���ʱ���ڣ�С������ľ���λ��֮����6:1
���𰸡�BD
��������
��ţ�ٵڶ����ɷֱ�������ٶȼ��ɣ����������ľ����ɵ�ϵͳ���ܵ��������ж϶����Ƿ��غ㡣�������ľ�徲ֹʱ���ɶ����غ㶨��������ߵĹ�ͬ�ٶȣ��������غ㶨�������ܡ�����![]() ����ľ�����С����L�����˶�ѧ��ʽ����ľ���λ��֮�ȡ�
����ľ�����С����L�����˶�ѧ��ʽ����ľ���λ��֮�ȡ�
A��������ˮƽ����ֻ�ܵ�Ħ���������ã���ţ�ٵڶ����ɿɵã�![]() ������⻬����֪M��ˮƽ����Ҳֻ�ܵ�m��M��Ħ��������ţ�ٵڶ�_���ɿɵã�
������⻬����֪M��ˮƽ����Ҳֻ�ܵ�m��M��Ħ��������ţ�ٵڶ�_���ɿɵã�![]() �����Ц��Ƕ���֮��Ķ�Ħ������������
�����Ц��Ƕ���֮��Ķ�Ħ������������![]() ����A����
����A����
B��ˮƽ��⻬�����ľ����ɵ�ϵͳ���ܵĺ�����Ϊ�㣬����ˮƽ�������غ㣬�������ľ�徲ֹʱ��ȡ����Ϊ�������ݶ����غ㶨�ɵã�![]() ����ã� v= 1m/s�����������غ㶨�ɵã������y������Ħ�����������ܣ�
����ã� v= 1m/s�����������غ㶨�ɵã������y������Ħ�����������ܣ�![]() ����B��ȷ��
����B��ȷ��
C����ľ�����С����ΪL���t��![]() �������ڲ�֪����Ħ������
�������ڲ�֪����Ħ������![]() ���������ľ�����С���ȣ���C����
���������ľ�����С���ȣ���C����
D.�ӿ�ʼ��������ľ��������ֹ�z�΅����ڣ�������ľ���λ��֮���ǣ�
![]() ����D��ȷ��
����D��ȷ��

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�