题目内容
(20分) 对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可简化为如下模型:两物体位于光滑水平面上,仅限于沿一直线运动,当它们之间距离大于某一定值d时,相互作用力为零,当它们之间的距离小于d时,存在大小恒为F的斥力
设物体A的质量m1="1.0kg," 开始静止在直线上某点,物体B的质量m2=3.0kg,以速度V0从远处沿直线向A运动,如图所示,若d="0.10m," F="0.60N," V0=0.20m/s,求:
相互作用过程中A、B 的加速度大小
从开始相互作用到A、B间距离最小时,系统(物体组)动能减少量
 A、B间的最小距离
A、B间的最小距离
设物体A的质量m1="1.0kg," 开始静止在直线上某点,物体B的质量m2=3.0kg,以速度V0从远处沿直线向A运动,如图所示,若d="0.10m," F="0.60N," V0=0.20m/s,求:
相互作用过程中A、B 的加速度大小
从开始相互作用到A、B间距离最小时,系统(物体组)动能减少量
 A、B间的最小距离
A、B间的最小距离解:( 1 ) 当两者距离小于d时,有恒力作用,由牛顿第二定律
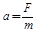 得:
得:对A:
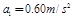 对B:
对B: 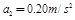
(2)两者速度相等时,距离最近,由动量守恒定律:
有:
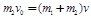
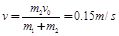
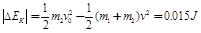
(3)有能的转换关系:
有:
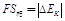
即:

所以
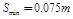
分析:(1)已知两球受到的力及各自质量,由牛顿第二定律可直接求得两球的加速度;
(2)由运动过程可知,当两球相距最近时,两速的速度相等,由动量守恒可求得此时的共同速度,即可求得动能的变化量;
(3)从开始到相距最近,两球均做匀变速直线运动,由速度关系可求得两球运动的时间,即可分别求得两球的位移,则可得出两球相距的最小值.
解答:解:(1)由F=ma可得:
A的加速度为:a1= F/m1=0.60m/s2
B的加速度为:a2= F/ m2=0.20m/s2;
A、B的加速度分别为0.60m/s2,0.20m/s2;
(2)两者速度相同时,距离最近,由动量守恒得:m2v0=(m1+m2)v
解得共同速度v= m2v0/(m1+m2) =0.15m/s
则动能的变化量: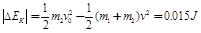 ;
;
即动能的变化量为0.015J;
(3)根据匀变速直线运动规律得
A的速度:v1=a1t
B的速度:v2=v0-a2t
因v1=v2,解得:
t=0.25s
则A的位移s1= a1t2/2
B的位移s2=v0t- a2t2/2
两物体的距离为△s=s1+d-s2
将t=0.25s代入,解得A、B间的最小距离△smin=0.075m
A、B间的最小距离为0.075m.
点评:本题属弹簧连接体模型的变型题,这种模型两物体之间有相互作用,但不受其它外力,满足动量守恒,从能量的观点看,系统的动能与势能相互转化,并且当两物体速度相等时,势能达到最大,动能损耗最多;不过本题简化成了物体做匀变速运动,同时也考查了动力学的相关知识,是道好题.
(2)由运动过程可知,当两球相距最近时,两速的速度相等,由动量守恒可求得此时的共同速度,即可求得动能的变化量;
(3)从开始到相距最近,两球均做匀变速直线运动,由速度关系可求得两球运动的时间,即可分别求得两球的位移,则可得出两球相距的最小值.
解答:解:(1)由F=ma可得:
A的加速度为:a1= F/m1=0.60m/s2
B的加速度为:a2= F/ m2=0.20m/s2;
A、B的加速度分别为0.60m/s2,0.20m/s2;
(2)两者速度相同时,距离最近,由动量守恒得:m2v0=(m1+m2)v
解得共同速度v= m2v0/(m1+m2) =0.15m/s
则动能的变化量:
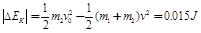 ;
;即动能的变化量为0.015J;
(3)根据匀变速直线运动规律得
A的速度:v1=a1t
B的速度:v2=v0-a2t
因v1=v2,解得:
t=0.25s
则A的位移s1= a1t2/2
B的位移s2=v0t- a2t2/2
两物体的距离为△s=s1+d-s2
将t=0.25s代入,解得A、B间的最小距离△smin=0.075m
A、B间的最小距离为0.075m.
点评:本题属弹簧连接体模型的变型题,这种模型两物体之间有相互作用,但不受其它外力,满足动量守恒,从能量的观点看,系统的动能与势能相互转化,并且当两物体速度相等时,势能达到最大,动能损耗最多;不过本题简化成了物体做匀变速运动,同时也考查了动力学的相关知识,是道好题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 。(g=l0m/s2)
。(g=l0m/s2)








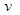 向Q运动,P、Q质量均为
向Q运动,P、Q质量均为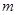 ,与轻位于簧发生碰撞的整个过程中,弹簧具有的最大弹性势能为多少?
,与轻位于簧发生碰撞的整个过程中,弹簧具有的最大弹性势能为多少?