题目内容
如图所示，在光滑水平面上有一辆质量M="8" kg的平板小车，车上有一个质量m=1．9 kg的木块，木块距小车左端6m（木块可视为质点），车与木块一起以v="1" m/s的速度水平向右匀速行驶。一颗质量m0=0．1kg的子弹以v0="179" m/s的初．速度水平向左飞来，瞬间击中木块并留在其中。如果木块刚好不从车上掉下来，求木块与平板小车之间的动摩擦因数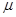
。（g=l0m／s2）
。（g=l0m／s2）解：设子弹射入木块后的共同速度为v1，以水平向左为正，则由动量守恒有：
m0v0-mv=（m+m0）v1 ……①----------（2分）
v1="8" m/s ----------（1分）
它们恰好不从小车上掉下来，则它们相对平板车滑行s=6m时它们跟小车具有共同速度v2，则由动量守恒有：
（m+m0）v1-Mv =（m+m0+M）v2 ……②--------（2分）
v2="0.8" m/s ----------（1分）
由能量守恒定律有：
Q=μ（m0+m）g s =
…③--------（2分）
由①②③，代入数据可求出µ=0.54 ----------（1分）
m0v0-mv=（m+m0）v1 ……①----------（2分）
v1="8" m/s ----------（1分）
它们恰好不从小车上掉下来，则它们相对平板车滑行s=6m时它们跟小车具有共同速度v2，则由动量守恒有：
（m+m0）v1-Mv =（m+m0+M）v2 ……②--------（2分）
v2="0.8" m/s ----------（1分）
由能量守恒定律有：
Q=μ（m0+m）g s =
…③--------（2分）由①②③，代入数据可求出µ=0.54 ----------（1分）
练习册系列答案
相关题目
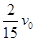
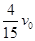
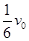
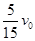
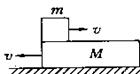
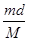
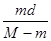
=0.5m，在B的右端有一个可以看作质点的小铁块C，三者的质量都为m，C与A、B间的动摩擦因数都为μ。现在A以速度ν0=6m/s向右运动并与B相碰，撞击时间极短，碰后A、B粘在一起运动，而C可以在A、B上滑动，问：如果μ=0.5，则C会不会掉下地面？
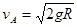。已知小球a质量为m，小球b质量为2m，重力加速度为g。求：
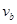的大小；
A、B间的最小距离